Altitude of equilateral triangle formula

The perpendicular drawn from the vertex to the opposite side of the triangle is called the altitude of a triangle. The altitude of a triangle formula gives us the height of the triangle. The altitude of a triangle formula is interpreted and different formulas are given for different types of triangles.

The equilateral triangle calculator will help you with calculations of standard triangle parameters. Whether you are looking for the equilateral triangle area, its height, perimeter, circumradius, or inradius, this great tool is a safe bet. Scroll down to read more about valuable formulas such as the one used to calculate the height of an equilateral triangle and learn what an equilateral triangle is. The equilateral triangle, also called a regular triangle, is a triangle with all three sides equal. What are the other important properties of that specific regular shape? The equilateral triangle is a special case of an isosceles triangle, having not just two but all three sides equal.

Altitude of equilateral triangle formula

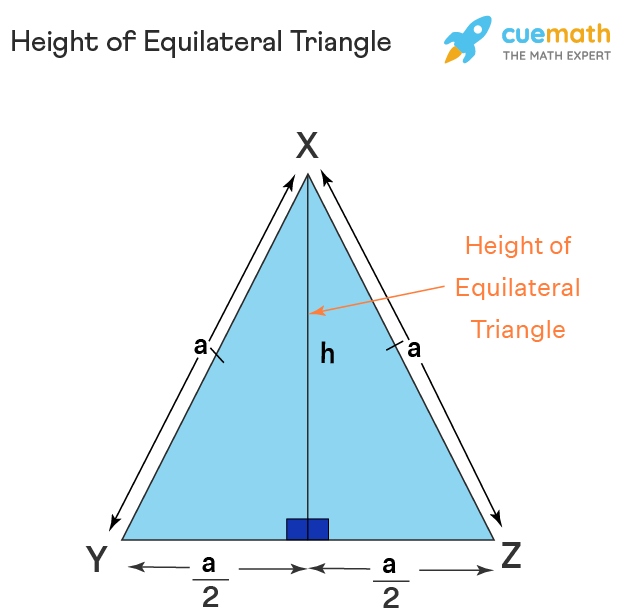
The height of an equilateral triangle is a straight line that is drawn from the vertex to the opposite side of the triangle in such a way that it divides the triangle into two equal right-angled triangles. This is also known as the altitude of the triangle which starts from the vertex and is the perpendicular bisector of the opposite side. An equilateral triangle is a triangle in which all the sides are of equal length and all the angles are of equal measure. Let us learn more about the height of equilateral triangle in this article. The height of an equilateral triangle is a line that is drawn from any vertex of the triangle on the opposite side. This line is the perpendicular bisector of the opposite side. The height of an equilateral triangle is also known as the altitude which divides the triangle into two congruent right-angled triangles as shown in the following figure. An Equilateral triangle is defined as a triangle where all three sides and angles are equal. The value of each angle is 60 degrees, therefore, it is also known as an equiangular triangle. The equilateral triangle is considered as a regular polygon because all its angles and sides are equal. The height of equilateral triangle can be calculated with the help of the Pythagoras theorem. The formula that is used to find the height of an equilateral triangle is,.

Contribute your expertise and make a difference in the GeeksforGeeks portal. An equilateral triangle is a geometrical 2D figure which has all three sides equal.

The internal angles of any given equilateral triangle are of the same measure, that is, equal to 60 degrees. Triangles are classified into three sorts based on the length of their sides:. Scalene triangle: The sides and the angles of the scalene triangle are not equal. Isosceles triangle: An isosceles triangle has two equal sides and two equal angles. Equilateral triangle: All sides and angles of the equilateral triangle are equal. The region enclosed by the three sides of an equilateral triangle is defined as the area of the equilateral triangle. It is expressed in square units.

The equilateral triangle calculator will help you with calculations of standard triangle parameters. Whether you are looking for the equilateral triangle area, its height, perimeter, circumradius, or inradius, this great tool is a safe bet. Scroll down to read more about valuable formulas such as the one used to calculate the height of an equilateral triangle and learn what an equilateral triangle is. The equilateral triangle, also called a regular triangle, is a triangle with all three sides equal. What are the other important properties of that specific regular shape? The equilateral triangle is a special case of an isosceles triangle, having not just two but all three sides equal. If you would like to learn more about the isosceles triangle, our isosceles triangle calculator is just the tool you need. The formula for a regular triangle area is equal to the squared side times the square root of 3 divided by But do you know where the formulas come from? You can find them in at least two ways: deriving from the Pythagorean theorem discussed in our Pythagorean theorem calculator or using trigonometry.

Altitude of equilateral triangle formula

The altitude of a triangle is the perpendicular line segment drawn from the vertex to the opposite side of the triangle. It may lie inside or outside the triangle, based on the types of triangles. The altitude of a triangle basically defines the height, when we have to measure the area of a triangle, with respect to the base. The altitude of a triangle is the perpendicular drawn from the vertex of the triangle to the opposite side. Also, known as the height of the triangle, the altitude makes a right-angle triangle with the base. The main application use of altitude is that it is used for area calculation of the triangle, i. The different properties of altitude of a triangle are listed below:. About altitude, different triangles have different types of altitude. Below is an overview of different types of altitudes in different triangles.

Taylor 214ce red dlx

The height of equilateral triangle can be calculated with the help of the Pythagoras theorem. What kind of Experience do you want to share? This regular triangle has all sides equal, so the formula for the perimeter is:. Hence, a right triangle can never be an equilateral triangle. Substituting the value of the given height 'h' in the formula, we can find the side 'a' of the triangle, and then the area can be calculated. People also viewed See all. Let us learn different altitude formulas on various different conditions for different types of triangles. Example 1: Find the height of an equilateral triangle if its side length is 3 units. It is also known that all the sides of an equilateral triangle are equal in length, therefore, if the perimeter is known, we can calculate the side length using this formula. Which kind of angle is between the smallest and the largest? Improve Improve.

The perpendicular drawn from the vertex to the opposite side of the triangle is called the altitude of a triangle.

Explore math program. With Cuemath, find solutions in simple and easy steps. What kind of Experience do you want to share? How to find the altitude of an equilateral triangle given the perimeter? We remember that all sides and all angles are equal in the equilateral triangle, so the formula simplifies to:. It is also known that all the sides of an equilateral triangle are equal in length, therefore, if the perimeter is known, we can calculate the side length using this formula. The altitude is used for the calculation of the area of a triangle. Open In App. It's working this way as well. Admission Experiences.