Area of triangular pyramid

A triangular pyramid has a triangle-shaped base and all three triangular faces meet at the apex. There is a special case of a triangular pyramid called a tetrahedron, area of triangular pyramid has equilateral triangles for each of the faces. The triangular pyramid formula consists of both the volume and the surface area of the triangular pyramid that calculates the three triangular-shaped sides, the height, and the slant height.

The surface area of a triangular pyramid is the total area of all faces of a triangular pyramid. Basically, a triangular pyramid has a triangular base and is bounded by three lateral triangular faces that meet at one vertex. A triangular pyramid has all faces as triangles. This pyramid has 4 faces, 6 edges, and 4 corners or vertices. Few types of the triangular pyramid are given below:. The surface area of any three-dimensional geometrical shape is the sum of the areas of all of the faces or surfaces of that enclosed solid.

Area of triangular pyramid

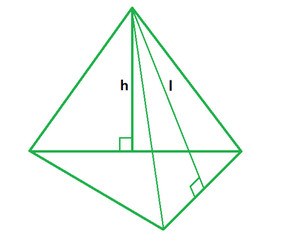
A solid with a triangular base such that the triangles have a common vertex on all three lateral sides is called a triangular pyramid. It can be interpreted as a tetrahedron with equilateral triangles on all four faces. It is a three-dimensional object with a triangle base and four triangular faces, three of which meet at one vertex. The base of a right triangular pyramid is a right-angled triangle, while the rest of the faces are isosceles triangles. The surface area of a triangular pyramid has two formulas, that is, lateral surface area and total surface area. It is calculated by adding the area of triangular faces with no base, i. It is equal to half the product of perimeter and slant height. It is computed by adding the area of all triangular faces of the pyramid. Its formula is equal to the sum of the base area and half the product of perimeter and slant height. It is the sum of the base area and lateral surface area of the pyramid. Problem 1: Find the lateral surface area of a triangular pyramid with a base of 10 m and a slant height of 12 m. Problem 2: Find the lateral surface area of a triangular pyramid with a base of 15 m and a slant height of 20 m. Problem 3: Find the base length of a triangular pyramid with a slant height of 12 m and a lateral area of sq. Problem 4: Find the slant length of a triangular pyramid with a base of 6 m and a lateral area of 81 sq.

What kind of Experience do you want to share?

The surface area of a triangular pyramid calculator is a free online tool that can be used to calculate the surface area of the pyramid as well as its base length, base height and slant height. Let us familiarize ourselves with the calculator. Read More Read Less. The steps that follow helps in using the surface area of a triangular pyramid calculator:. Step 1: Enter any two known measures into the respective input boxes and the unknown measures will be calculated. Step 2: Select the appropriate units for the input and output.

Created By : Abhinandan Kumar. Reviewed By : Rajashekhar Valipishetty. Last Updated : Apr 21, Surface area of a Pyramid - The surface area of a pyramid is equal to the sum of the areas of each side of the pyramid. The base of the pyramid has area l w , and sl and sw represent the slant height on the length and slant height on the width. Surface Area of a Pyramid Calculator: Are you looking for the process on how to find the surface area of a pyramid? Then, you are on the right page.

Area of triangular pyramid

Just as you can have a triangular pyramid, you can also have a rectangular pyramid, a pentagonal pyramid, etc. The Great Pyramids of Egypt in Giza, for example, is a square pyramid because its base bottom is a square. A triangular pyramid is a pyramid with a triangular base. A pyramid with an equilateral triangle base is a regular triangular pyramid. If a scalene or isosceles triangle forms the base, then the pyramid is a non-regular triangular pyramid. No rule requires the base of a triangular pyramid to be an equilateral triangle, though constructing scalene or isosceles triangular pyramids is far harder than constructing an equilateral triangular pyramid. Two different surface area measurements can be taken for any 3D solid: the lateral surface area and the surface area.

What level does abra evolve in fire red

What is a triangular pyramid? The following figure shows how a triangular pyramid looks like: What is Triangular Pyramid Formula? Pre-Algebra Tutors near me. The triangular pyramid formula consists of both the volume and the surface area of the triangular pyramid that calculates the three triangular-shaped sides, the height, and the slant height. Let us familiarize ourselves with the calculator. Add to Find the Area Game. The surface area of any three-dimensional geometrical shape is the sum of the areas of all of the faces or surfaces of that enclosed solid. Statistics Tutors near me. The slant height of the triangular pyramid is 6 centimeters and the height of its base is 3. Engineering Exam Experiences. It is a three-dimensional object with a triangle base and four triangular faces, three of which meet at one vertex. Easy Normal Medium Hard Expert.

The surface area of triangular pyramid calculator handles all pyramid related calculations like a pro. It offers a one-stop-shop for all calculations of a pyramid. A pyramid is a solid object having a polygon base and triangular sides that meet at the top.

Contribute to the GeeksforGeeks community and help create better learning resources for all. Skip to content. Q5: Find the surface area of a triangular pyramid whose area of the base triangles is 24 sq. Submit your entries in Dev Scripter today. A tetrahedron is a triangular pyramid in which all the faces are triangles of equal size. It can be calculated by subtracting the base from the total surface area. Arithmetic Tutors near me. Please note that, with the fraction as a factor in our multiplication, we do not have a precise decimal answer, so we have an approximate value. A solid with a triangular base such that the triangles have a common vertex on all three lateral sides is called a triangular pyramid. Problem 1: Find the lateral surface area of a triangular pyramid with a base of 10 m and a slant height of 12 m.