Cantors paradise

This is the continuation of the installment published four weeks ago. Kevin Buzzard was the guest. For the most part the notes have not been amended, cantors paradise, but I have added some additional material to explain allusions to earlier sessions of the course. Human intelligence cantors paradise to the mechanical level, kindling the idea of machine intelligence.

Cantor's Archive is an official directory of stories published in Cantor's Paradise, a Medium publication of math-related essays. Cantor's Archive includes stories published in Cantor's Paradise which are older than 1 years old. Stories are archived monthly and we expect to be up-to-date with old stories by June of Medium ceased supporting publications in mid The company has yet to make a profit. In venture capital terms, one might describe the company as one that is "living dead".

Cantors paradise

This article is a runner up in the general public category of the Plus new writers award Modern ideas about infinity provide a wonderful playground for mathematicians and philosophers. I want to lead you through this garden of intellectual delights and tell you about the man who created it — Georg Cantor. Cantor was born in Russia in When he was eleven years old his family moved to Germany and he suffered from a wistful homesickness for the rest of his life. At school he had a great talent for the violin, but his real gift and passion was for mathematics. As a university student in Berlin he was president of the mathematical society and met his friends every week in a wine house In he was appointed extraordinary professor at Halle, and began his life-long study of infinite sets. The diagram shows that there is a one-to-one correspondence , or bijection , between the two sets. Since each element in pairs off with one element in and vice versa, the sets must have the same "size", or, to use Cantor's language, the same cardinality. Using a bijection to compare the size of two infinite sets was one of Cantor's most fruitful ideas.

For the most part the notes have not been amended, cantors paradise, but I have added some additional material to explain allusions to earlier sessions of the course.

.

In the history of mathematics and economics, Karl Menger is a fairly anonymous figure. This, perhaps, for a few reasons. Although he was a prodigy, Karl was also the son of another great mind, Carl Menger At the age of 24, he revolutionized our understanding of the limits of epistemology — the theory of knowledge—by proving mathematically that all formal systems of logic are inherently incomplete. By the late s, the favorite past-time of faculty and graduate students in Fine Hall at Princeton University was board games, including the famous Go and Chess, as well as the less famous Kriegspiel. On November 29th, mathematician Georg Cantor sent a letter to Richard Dedekind asking whether or not the collection of natural numbers and the collection of positive real numbers A mere 24 years old, Werner Heisenberg in developed a treatment of electron behavior based solely on directly observable quantities such as the frequencies of light that atoms absorb and emit. Beloved late physicist Richard P. Mathematics Karl Menger's Vienna Colloquium In the history of mathematics and economics, Karl Menger is a fairly anonymous figure.

Cantors paradise

This article is a runner up in the general public category of the Plus new writers award Modern ideas about infinity provide a wonderful playground for mathematicians and philosophers. I want to lead you through this garden of intellectual delights and tell you about the man who created it — Georg Cantor.

Arzu restaurant

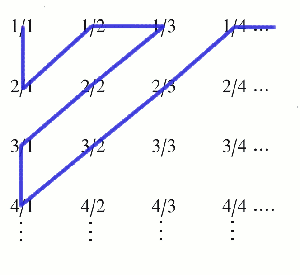
What was optimal for human minds was not optimal for machines … at the level of the procedures required to mesh human and machines in long sequences of calculation, whether in the offices of the Nautical Almanac or the French Railways, tasks previously conceived holistically and executed by one calculator had to be analyzed into their smallest component parts, rigidly sequenced, and apportioned to the human or mechanical calculator able to execute that step most efficiently — where efficiently meant not better or even faster but cheaper. From onwards, Cantor suffered from bouts of depression during which he could not concentrate on mathematics. Today this amazing conclusion is honoured with the title Cantor's theorem , but in his own day most mathematicians did not understand it. Conjecture Christian Goldbach, : Every even number greater than 2 is the sum of two prime numbers. Ninety-four days later, in my dream, Tom's simulacrum remarked, "The direct limit characterization of perfect complexes shows that they extend, just as one extends a coherent sheaf. This is a divergent problem handled badly. Georg Cantor. Modern ideas about infinity provide a wonderful playground for mathematicians and philosophers. Cantor had shown that was greater than — but was it equal to the next cardinal number on the list,? Another Cantor related subject is the Cantor set, generated by taking the number line between 0 and 1 and removing the open inner third part an infinite number of times. Please turn on JavaScript or unblock scripts. Text within this block will maintain its original spacing when published Mathematics and narrative, 2. Imagine such a list:.

.

Cantor's Archive, however, is hosted on Ghost, an open source blogging platform. Please turn on JavaScript or unblock scripts. Read more about At the time Cantor's Paradise was founded, Medium was still investing in building new features and supporting new publications. Analyzing how the term is used, I am led to the tentative conclusion that it refers to the branch of mathematics concerned with objects that can be legitimately, or systematically, designated by the letter K. He degrades and simplifies the client. His old professor, Leopold Kronecker said. Dec 01, Because of this simple bijection with the natural numbers, all infinite countable sets have cardinality. Peter studied mathematics and physics at the University of St. The cardinality of is not of course an ordinary number, since is infinite. Cantor's Archive is an official directory of stories published in Cantor's Paradise, a Medium publication of math-related essays. The set of real numbers contains both the natural numbers and the rational numbers, but is it really "bigger" than both these sets?