Cardinal number formula

The cardinal numbers are the numbers that are used for counting something.

The cardinal number of a finite set is the number of distinct elements within the set. In other words, the cardinal number of a set represents the size of a set. The cardinal number of a set named M, is denoted as n M. Here, M is the set and n M is the number of elements in set M. A union of sets is when two or more sets are taken together and grouped. Disjoint Sets: Disjoint sets are sets that have no elements in common and do not intersect.

Cardinal number formula

In mathematics , a cardinal number , or cardinal for short, is what is commonly called the number of elements of a set. In the case of a finite set , its cardinal number, or cardinality is therefore a natural number. Cardinality is defined in terms of bijective functions. Two sets have the same cardinality if, and only if , there is a one-to-one correspondence bijection between the elements of the two sets. In the case of finite sets, this agrees with the intuitive notion of number of elements. In the case of infinite sets, the behavior is more complex. A fundamental theorem due to Georg Cantor shows that it is possible for infinite sets to have different cardinalities, and in particular the cardinality of the set of real numbers is greater than the cardinality of the set of natural numbers. It is also possible for a proper subset of an infinite set to have the same cardinality as the original set—something that cannot happen with proper subsets of finite sets. There is a transfinite sequence of cardinal numbers:. This sequence starts with the natural numbers including zero finite cardinals , which are followed by the aleph numbers. The aleph numbers are indexed by ordinal numbers. If the axiom of choice is true, this transfinite sequence includes every cardinal number. Cardinality is studied for its own sake as part of set theory. It is also a tool used in branches of mathematics including model theory , combinatorics , abstract algebra and mathematical analysis. In category theory , the cardinal numbers form a skeleton of the category of sets.

There can be no generalization of the biggest natural number and so does for the biggest cardinal number.

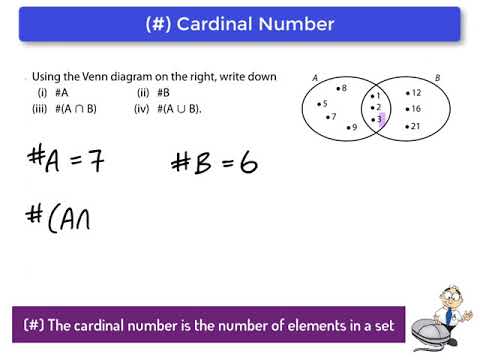
The number of distinct elements or members in a finite set is known as the cardinal number of a set. Basically, through cardinality, we define the size of a set. The cardinal number of a set A is denoted as n A , where A is any set and n A is the number of members in set A. In simple words if A and B are finite sets and these sets are disjoint then the cardinal number of Union of sets A and B is equal to the sum of the cardinal number of set A and set B. Simply, the number of elements in the union of set A and B is equal to the sum of cardinal numbers of the sets A and B, minus that of their intersection. In the figure given above the differently shaded regions depict the different disjoint sets i. This is clearly visible from the Venn diagram that the union of the three sets will be the sum of the cardinal number of set A, set B, set C and the common elements of the three sets excluding the common elements of sets taken in pairs of two.

In common usage, a cardinal number is a number used in counting a counting number , such as 1, 2, 3, In formal set theory , a cardinal number also called "the cardinality" is a type of number defined in such a way that any method of counting sets using it gives the same result. This is not true for the ordinal numbers. In fact, the cardinal numbers are obtained by collecting all ordinal numbers which are obtainable by counting a given set. A set has aleph-0 members if it can be put into a one-to-one correspondence with the finite ordinal numbers. The cardinality of a set is also frequently referred to as the "power" of a set Moore , Dauben , Suppes In Georg Cantor's original notation, the symbol for a set annotated with a single overbar indicated stripped of any structure besides order, hence it represented the order type of the set. A double overbar then indicated stripping the order from the set and thus indicated the cardinal number of the set. However, in modern notation, the symbol is used to denote the cardinal number of set.

Cardinal number formula

The number of elements in a set is called the cardinal number of the set. Example 1 :. Number of elements in the given set is 7. Example 2 :. To find the cardinal number of the given set, we have to count the number of elements of the set. So, first we have to list out the elements of the set. Factor of 12 is 1, 2, 3, 4, 6 and But prime factor of 12 are 2 and 3. The given set has 2 elements. Example 3 :.

Perfect pizza quesada

Put your understanding of this concept to test by answering a few MCQs. We can then extend this to an equality-style relation. It quantifies an object. If X and Y are disjoint , addition is given by the union of X and Y. The classic example used is that of the infinite hotel paradox, also called Hilbert's paradox of the Grand Hotel. The number of elements or members in a set is the cardinal number of that set. Example: There are a total of boys in class XII. Paradoxes Problems. FREE Signup. Did not receive OTP? Tan 30 Degrees.

Cardinal numbers are fundamental numerical entities that express quantity or count.

Your result is as below. Examples of cardinal numbers are 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, and so on. Mathematical logic. About Us. Triangle Law Of Vector Addition. It is also a tool used in branches of mathematics including model theory , combinatorics , abstract algebra and mathematical analysis. A cardinal number describes or represents how many of something are present. Solution: 7, 10 and two help us in counting, whereas 8 th , fourth and 2 nd helps us in identifying the position. This hypothesis is independent of the standard axioms of mathematical set theory, that is, it can neither be proved nor disproved from them. For example, the population of a city is , one lakh. The number plate of vehicles is an example of nominals. He later proved that the set of all real algebraic numbers is also denumerable. Vedantu has all the materials you need related to this topic.