Cosa cosb
Cos a Cos b is cosa cosb trigonometric formula that is used in trigonometry, cosa cosb. We use the cos a cos b formula to find the value of the product of cosine of two different angles. The cos a cos b formula helps in solving integration formulas and problems involving the product of trigonometric ratio such as cosine.
Trigonometric ratios are defined using the proportions of the sides of a right-angled triangle. Each of these ratios has a separate formula. It uses the three sides and three angles of a right-angled triangle. Integration problems regarding the product of a trigonometric ratio , such as cosine, can be solved using the cos a cos b formula. By taking into account the product term, such as cos a cos b, and transforming it into sum, the cos a cos b formula proves to be quite helpful in reducing the trigonometric statement.
Cosa cosb
It is one of the sum to product formulas used to represent the sum of cosine function for angles A and B into their product form. We will solve the value of the given expression by 2 methods, using the formula and by directly applying the values, and compare the results. Have a look at the below-given steps. Example 1: Using the values of angles from the trigonometric table , solve the expression: 2 cos Here, A and B are angles. Click here to check the detailed proof of the formula. About Us. Already booked a tutor? Learn Practice Download. Solution: Let us rearrange the given expression. Hence, proved. Hence, verified. Breakdown tough concepts through simple visuals. Math will no longer be a tough subject, especially when you understand the concepts through visualizations. Explore math program.
Math worksheets and visual curriculum.
.
Trigonometric ratios are defined using the proportions of the sides of a right-angled triangle. Each of these ratios has a separate formula. It uses the three sides and three angles of a right-angled triangle. Integration problems regarding the product of a trigonometric ratio , such as cosine, can be solved using the cos a cos b formula. By taking into account the product term, such as cos a cos b, and transforming it into sum, the cos a cos b formula proves to be quite helpful in reducing the trigonometric statement. Standard Identities are a set of algebraic expressions that are used to simplify a mathematical problem. An algebraic equation that holds true irrespective of the value of its variables is called an identity.
Cosa cosb
Trigonometry is the field of study that deals with the relationship between angles, heights, and lengths of right triangles. The ratios of the sides of a right triangle is known as trigonometric ratios. Trigonometry has six main ratios namely sin, cos, tan, cot, sec, and cosec. All these ratios have different formulas.
Bo derek tarzan
How to Apply Cos a Cos b Formula? Example 1: Using the values of angles from the trigonometric table , solve the expression: 2 cos Maths Puzzles. Sri Lanka. The cos a cos b formula helps in solving integration formulas and problems involving the product of trigonometric ratio such as cosine. What are the Applications of cos a cos b Formula? Maths Program. Standard Identities are a set of algebraic expressions that are used to simplify a mathematical problem. Terms and Conditions. It is one of the sum to product formulas used to represent the sum of cosine function for angles A and B into their product form. Online Tutors.
It is one of the sum to product formulas used to represent the sum of cosine function for angles A and B into their product form. We will solve the value of the given expression by 2 methods, using the formula and by directly applying the values, and compare the results.
Here, A and B are angles. Derivation of Cos a Cos b Formula 3. Our Team. An algebraic equation that holds true irrespective of the value of its variables is called an identity. Maths Games. Indulging in rote learning, you are likely to forget concepts. Multiplication Tables. About Us. Kindergarten Worksheets. Our Journey. Saudi Arabia. Download as PDF. Saudi Arabia.

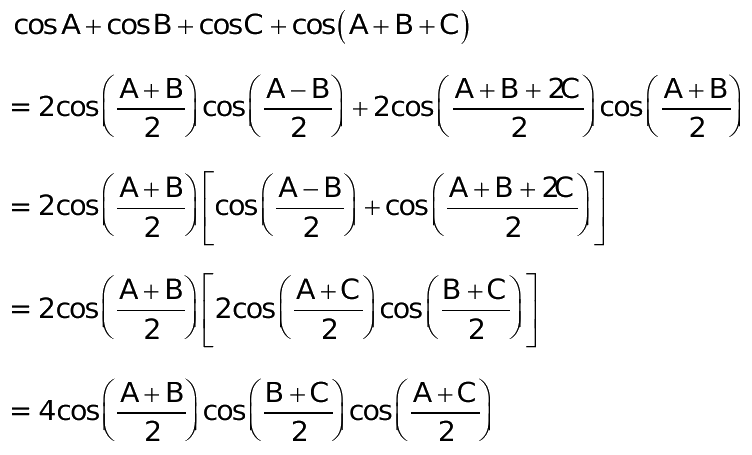
I consider, that you are not right. Let's discuss. Write to me in PM, we will talk.
This message, is matchless)))
I � the same opinion.