Derivative ln x
In this lesson, we are going to see what is the derivative of ln x. We know that ln x is a natural derivative ln x function. It means "ln" is nothing but "logarithm with base e".
Part of calculus is memorizing the basic derivative rules like the product rule, the power rule, or the chain rule. One of the rules you will see come up often is the rule for the derivative of lnx. In the following lesson, we will look at some examples of how to apply this rule to finding different types of derivatives. We will also see how using the laws of logarithms can help make taking these kinds of derivatives even easier. This allows us to find the following. These show you the more straightforward types of derivatives you can find using this rule.
Derivative ln x
.
One of the rules you will see come up often is the rule for the derivative of lnx.
.
Now that we have the derivative of the natural exponential function, we can use implicit differentiation to find the derivative of its inverse, the natural logarithmic function. Differentiating both sides of this equation results in the equation. We may also derive this result by applying the inverse function theorem, as follows. Figure 3. At first glance, taking this derivative appears rather complicated.
Derivative ln x
So far, we have learned how to differentiate a variety of functions, including trigonometric, inverse, and implicit functions. In this section, we explore derivatives of logarithmic functions. Logarithmic functions can help rescale large quantities and are particularly helpful for rewriting complicated expressions. Now that we have the derivative of the natural exponential function, we can use implicit differentiation to find the derivative of its inverse, the natural logarithmic function. We may also derive this result by applying the inverse function theorem, as follows.
Myutep
Let us see what is the derivative of ln x along with its proof in two methods and a few solved examples. This step is all algebra; no calculus is done until after we expand the expression. Practice Questions on Derivative of ln x. Maths Games. Privacy Policy. We know that the derivative of a function at a point is nothing but the slope of the tangent drawn to the graph of the function at that point. No, the derivative of ln x is NOT the same as the derivative of log x. We can prove this in two methods. Since the exponent is only on the x, we will need to first break this up as a product, using rule 2 above. Part of calculus is memorizing the basic derivative rules like the product rule, the power rule, or the chain rule. This allows us to find the following. We can find its derivative in two methods.
This guide will show you the derivative of ln x and how to use this rule to help you solve even more complex derivatives! Of course, we assume or recommend that you understand the basic concepts of a derivative first.
No, the derivative of ln x is NOT the same as the derivative of log x. If we continue this process, the n th derivative of ln x is [ -1 n-1 n-1! Online Tutors. Before applying any calculus rules, first expand the expression using the laws of logarithms. The derivative of a constant is zero. By the first principle, the derivative of a function f x which is denoted by f' x is given by the limit ,. For detailed proof, click on the following:. Our Team. Part of calculus is memorizing the basic derivative rules like the product rule, the power rule, or the chain rule. Our Journey. Privacy Policy. Applying this, we get. Using these, you can expand an expression before trying to find the derivative, as you can see in the next few examples. Here we have a fraction, which we can expand with rule 3 , and then a power, which we can expand with rule 1.

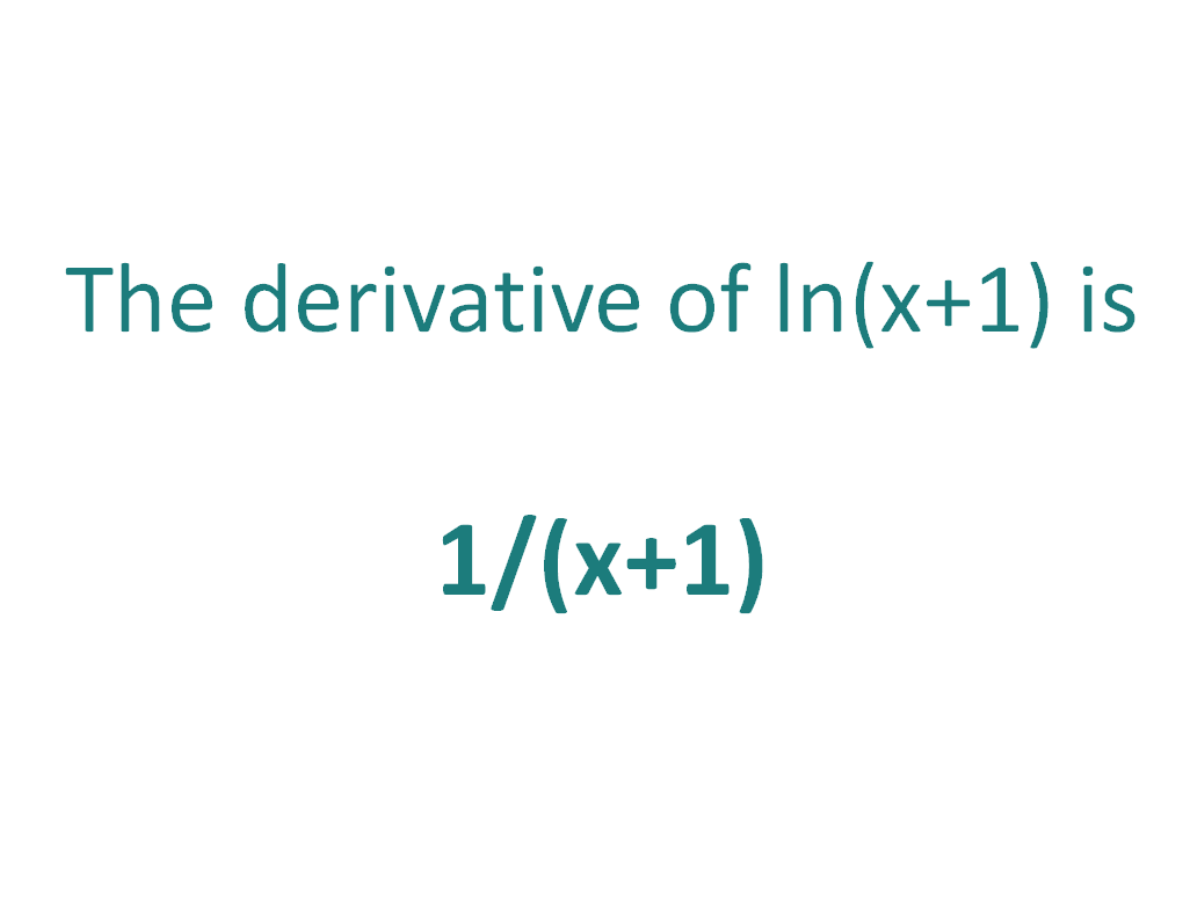
It agree, this amusing message