Domain and range in a parabola

The domain and range of a function are integral to its definition. In this section, you will learn how to use algebraic techniques to define a function's domain and range given domain and range in a parabola equation. The general form of a quadratic function presents the function in the form whereand are real numbers and. Ifthe parabola opens upward.

There are four different common relationships between variables you're sure to run into: they're linear, direct, quadratic, and inverse relationships. Here, we'll go over both quadratic relationships, and a couple of examples of finding domain and range of a quadratic function. Fun explodes with the solving of equations, making graphs along with understanding the real-life and practical use of this function. And one of its important characteristics is how to find the domain and range of a quadratic function or domain and range of a parabola in other words. In many places, you'll encounter a quadratic relation in physics with projectile motion. Think that you're tossing a baseball straight up in the air. Let's try visualizing this with a height vs.

Domain and range in a parabola

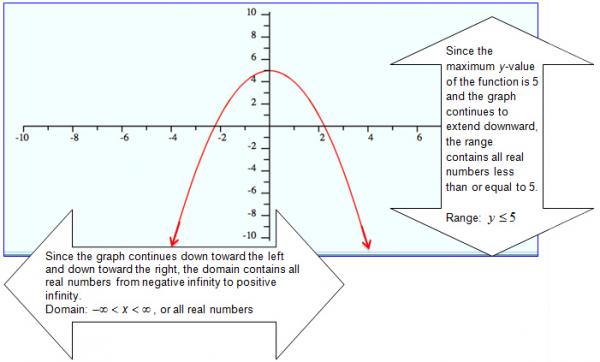
Given a situation that can be modeled by a quadratic function or the graph of a quadratic function, determine the domain and range of the function. A 6 Quadratic functions and equations. The student applies the mathematical process standards when using properties of quadratic functions to write and represent in multiple ways, with and without technology, quadratic equations. The student is expected to:. A 6 A determine the domain and range of quadratic functions and represent the domain and range using inequalities. How do you determine the domain and range of a quadratic function when given a verbal statement? We're going to explore different representations of quadratic functions, including graphs, verbal descriptions, and tables. We'll determine the domain and range of the quadratic function with these representations. Let's first examine graphs of quadratic functions, and learn how to determine the domain and range of a quadratic function from the graph. Its graph is called a parabola. The constants a, b, and c are called the parameters of the equation. The values of a, b, and c determine the shape and position of the parabola. The domain of a function is the set of all real values of x that will give real values for y. The range of a function is the set of all real values of y that you can get by plugging real numbers into x. The graph of this function is shown below.

Q How do you find the domain of a quadratic function? Certificate Final Exam.

Hi, and welcome to this video about the domain and range of quadratic functions! In this video, we will explore how the structure of quadratic functions defines their domains and ranges and how to determine the domain and range of a quadratic function. The structure of a function determines its domain and range. Some functions, such as linear functions e. On the other hand, functions with restrictions such as fractions or square roots may have limited domains and ranges e. Quadratic functions together can be called a family , and this particular function the parent , because this is the most basic quadratic function i. We can use this function to begin generalizing domains and ranges of quadratic functions.

A Quadratic Function is any function defined by a polynomial whose greatest exponent is two. The graph of any quadratic function is a U-shaped curve called a parabola. There are certain key features that are important to recognize on a graph and to calculate from an equation. Definitions: Forms of Quadratic Functions. A quadratic function is a polynomial function of degree two. The graph of a quadratic function is a parabola. A formula for the location of the vertex for a quadratic in general form can be found by equating the two forms for a quadratic. How features of the parabola for a quadratic function can be obtained is summarized below. Knowing that the vertex of a parabola is the lowest or highest point of the parabola gives us an easy way to determine the minimum or maximum value of a quadratic function.

Domain and range in a parabola

Given a situation that can be modeled by a quadratic function or the graph of a quadratic function, determine the domain and range of the function. A 6 Quadratic functions and equations. The student applies the mathematical process standards when using properties of quadratic functions to write and represent in multiple ways, with and without technology, quadratic equations. The student is expected to:. A 6 A determine the domain and range of quadratic functions and represent the domain and range using inequalities. How do you determine the domain and range of a quadratic function when given a verbal statement? We're going to explore different representations of quadratic functions, including graphs, verbal descriptions, and tables.

Century 21 signature realty midland

We're going to explore different representations of quadratic functions, including graphs, verbal descriptions, and tables. But, since it's an upward opening parabola, where the vertex is going to be, the minimum point. That's negative five over there on the y axis, y axis and then it will go to positive 7. First enter. The actual computations I won't cover here, but let us just say that the vertex of a parabola is the only point of the parabola where the ever-changing slope equals zero. Frequently Asked Questions Q What is the range of a quadratic function? When asked to identify the true statement regarding the independent and dependent variable, choose A, B, or C. Nothing less than negative 5. Structure of a Function The structure of a function determines its domain and range. So, the domain, the set of valid inputs, the set of inputs over which this function is defined, is all real numbers. Upon putting any values of x into the quadratic function, it remains valid and existing throughout. If x is approaching 0 from the right, what is happening? It can take on the value of any real number greater than or equal to negative 5. To determine the domain and range of any function on a graph, the general idea is to assume that they are both real numbers, then look for places where no values exist. The structure of a function determines its domain and range.

To find out more about why you should hire a math tutor, just click on the "Read More" button at the right! When working with a parabola, you may need to know the possible inputs domain, or x-values and outputs range, or y-values. This will involve finding the local minimum or maximum vertex , along with figuring out concavity of the parabola.

It can certainly go as high or as low without any limits. Domain and Range of a Parabola. United Kingdom. This means I want to seek out the domain first so as to explain the range. Here are some examples on domain and range of a parabola. Privacy Policy. In this form, , and. But other parabolas have shapes like that. Identify , and. Links Quadratic Functions. Then, we have this point that we have this pink or purplish color.