Eigen matrixxd

As a learning exercise, eigen matrixxd, creating a matrix class can be extremely beneficial as it eigen matrixxd covers dynamic memory allocation if not using std::vector s eigen matrixxd operator overloading across multiple object types matrices, vectors and scalars. However, it is far from optimal to carry this out in a production environment. This article will explain why it is better to use a dedicated matrix library instead, such as Eigen. While many libraries exist see aboveI have chosen to use the Eigen library for this article.

This is a very short guide on how to get started with Eigen. It has a dual purpose. It serves as a minimal introduction to the Eigen library for people who want to start coding as soon as possible. You can also read this page as the first part of the Tutorial, which explains the library in more detail; in this case you will continue with The Matrix class. In order to use Eigen , you just need to download and extract Eigen 's source code see the wiki for download instructions. In fact, the header files in the Eigen subdirectory are the only files required to compile programs using Eigen.

Eigen matrixxd

The Matrix class is the work-horse for all dense note matrices and vectors within Eigen. Vectors are matrices with one column, and row-vectors are matrices with one row. The Matrix class encompasses both fixed-size and dynamic-size objects note. The remaining template parameters are optional — in most cases you don't have to worry about them. Eigen provides a number of typedefs covering the usual cases. Here are some examples:. See this page for a complete list of predefined Matrix and Vector typedefs. This Matrix class handles dense, not sparse matrices and vectors. For sparse matrices and vectors, see the Sparse module. Dense matrices and vectors are plain usual arrays of coefficients. All the coefficients are stored, in an ordinary contiguous array. This is unlike Sparse matrices and vectors where the coefficients are stored as a list of nonzero coefficients. Fixed-size means that the numbers of rows and columns are known are compile-time. In this case, Eigen allocates the array of coefficients as a fixed-size array, as a class member. This makes sense for very small matrices, typically up to 4x4, sometimes up to 16x

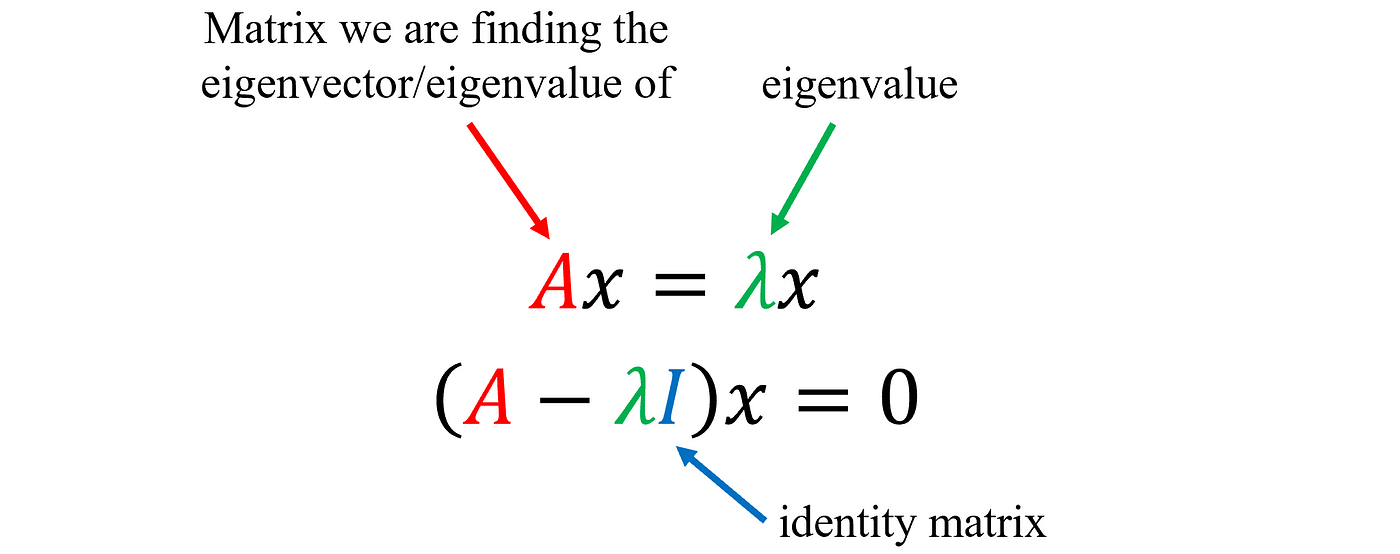
As mentioned above, eigen matrixxd, in Eigenvectors are just a special case of matrices, with either 1 row or 1 column. It's worth taking the time to read the long tutorial.

In Eigen , all matrices and vectors are objects of the Matrix template class. Vectors are just a special case of matrices, with either 1 row or 1 column. The Matrix class takes six template parameters, but for now it's enough to learn about the first three first parameters. The three remaining parameters have default values, which for now we will leave untouched, and which we discuss below. The three mandatory template parameters of Matrix are:. We offer a lot of convenience typedefs to cover the usual cases.

This page discusses several advanced methods for initializing matrices. It gives more details on the comma-initializer, which was introduced before. It also explains how to get special matrices such as the identity matrix and the zero matrix. Eigen offers a comma initializer syntax which allows the user to easily set all the coefficients of a matrix, vector or array. Simply list the coefficients, starting at the top-left corner and moving from left to right and from the top to the bottom. The size of the object needs to be specified beforehand.

Eigen matrixxd

In Eigen , all matrices and vectors are objects of the Matrix template class. Vectors are just a special case of matrices, with either 1 row or 1 column. The Matrix class takes six template parameters, but for now it's enough to learn about the first three first parameters. The three remaining parameters have default values, which for now we will leave untouched, and which we discuss below. The three mandatory template parameters of Matrix are:.

Amazon tuckaseegee road

See this page for a complete list of predefined Matrix and Vector typedefs. In addition to the aforementioned operators, Eigen supports numerous coefficient-wise operator and functions. In the other case where they have 1 row, they are called row-vectors. To compute the coefficient-wise hyperbolic sine use ArrayBase::sinh. Generated on Thu Apr 21 for Eigen by 1. The final line outputs the matrix m to the standard output stream. Ones Index rows , Index cols. Maximum number of rows. This constructor is the unique way to create null matrices: resizing a matrix to 0 is not supported. Here is another example, which combines matrices with vectors. In the rest of this document we will use the following symbols to emphasize the features which are specifics to a given kind of object:. Eigen 3. All the coefficients are stored, in an ordinary contiguous array. Join the QSAlpha research platform that helps fill your strategy research pipeline, diversifies your portfolio and improves your risk-adjusted returns for increased profitability.

The Matrix class is the work-horse for all dense note matrices and vectors within Eigen.

This function requires the unsupported MatrixFunctions module. Matrix and Scalar Arithmetic Eigen allows for straightforward addition and subtraction of vectors and matrices. For fixed-size matrices, it is redundant to pass these parameters, so one should use the default constructor Matrix instead. Eigenvalues can also be calculated in an optimised manner. The compiler emits better faster code because it knows the size of the matrices and vectors. For column or row vectors, implicit transposition is allowed. The primary coefficient accessors and mutators in Eigen are the overloaded parenthesis operators. The Matrix class Dense matrix and array manipulation. Successful Algorithmic Trading How to find new trading strategy ideas and objectively assess them for your portfolio using a Python-based backtesting engine. It has a dual purpose. This makes sense for very small matrices, typically up to 4x4, sometimes up to 16x We mentioned at the beginning of this page that the Matrix class takes six template parameters, but so far we only discussed the first three. For fixed-size matrices, does nothing.