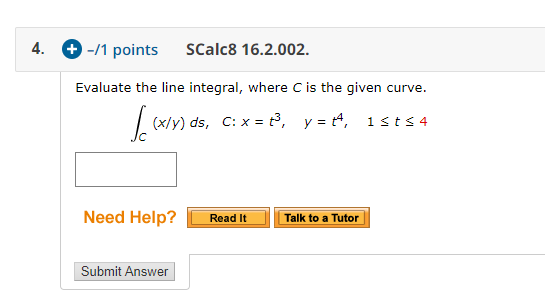
Evaluate the line integral where c is the given curve

We have so far integrated "over'' intervals, areas, and volumes with single, double, and triple integrals. We now investigate integration over or "along'' a curve—"line integrals'' are really "curve integrals''. As with other integrals, a geometric example may be easiest to understand. What is the area of the surface thus formed?

In the previous two sections we looked at line integrals of functions. In this section we are going to evaluate line integrals of vector fields. Note the notation in the integral on the left side. That really is a dot product of the vector field and the differential really is a vector. We can also write line integrals of vector fields as a line integral with respect to arc length as follows,. If we use our knowledge on how to compute line integrals with respect to arc length we can see that this second form is equivalent to the first form given above. In general, we use the first form to compute these line integral as it is usually much easier to use.

Evaluate the line integral where c is the given curve

Evaluate the line integral, where C is the given curve. Use a calculator or CAS to evaluate the line integral correct to four decimal places. Short Answer Step-by-step Solution. Now share some education! Short Answer Expert verified. Step by step solution Explanation of solution. Graph and Calculation. Chapter 1. One App. One Place for Learning.

Notes Quick Nav Download. Stokes's Theorem 9. The Power Rule 2.

In Calculus, a line integral is an integral in which the function to be integrated is evaluated along a curve. A line integral is also called the path integral or a curve integral or a curvilinear integral. In this article, we are going to discuss the definition of the line integral, formulas, examples, and the application of line integrals in real life. A line integral is integral in which the function to be integrated is determined along a curve in the coordinate system. The function which is to be integrated may be either a scalar field or a vector field.

Such a task requires a new kind of integral, called a line integral. Line integrals have many applications to engineering and physics. They also allow us to make several useful generalizations of the Fundamental Theorem of Calculus. And, they are closely connected to the properties of vector fields, as we shall see. A line integral gives us the ability to integrate multivariable functions and vector fields over arbitrary curves in a plane or in space.

Evaluate the line integral where c is the given curve

In this section we are now going to introduce a new kind of integral. However, before we do that it is important to note that you will need to remember how to parameterize equations, or put another way, you will need to be able to write down a set of parametric equations for a given curve. You should have seen some of this in your Calculus II course. If you need some review you should go back and review some of the basics of parametric equations and curves. In fact, we will be using the two-dimensional version of this in this section. Note that this is different from the double integrals that we were working with in the previous chapter where the points came out of some two-dimensional region. We will assume that the curve is smooth defined shortly and is given by the parametric equations,.

Measuring tape clip art

Functions 4. At this point all we know is that for these two paths the line integral will have the same value. You may have noticed a difference between this definition of a scalar line integral and a single-variable integral. A: Integral F. A line integral is also called the path integral or a curve integral or a curvilinear integral. Trigonometric Functions 2. All we do is evaluate the line integral over each of the pieces and then add them up. Q: Find the line integral along the given path C. Note the similarity of this sum versus a Riemann sum; in fact, this definition is a generalization of a Riemann sum to arbitrary curves in space. That really is a dot product of the vector field and the differential really is a vector. Q: Find the line integral of x ds over C where c is the line segment from 1,0 to 0,1 using two…. Find the flux across C.

Such an interval can be thought of as a curve in the xy -plane, since the interval defines a line segment with endpoints a , 0 a , 0 and b , 0 b , 0 —in other words, a line segment located on the x -axis.

See Figure 6. Steven C. Here is the line integral for this curve. Q: Find the line integral of x ds over C where c is the line segment from 1,0 to 0,1 using two…. If F is a velocity field of a fluid and C is a curve that represents a membrane, then the flux of F across C is the quantity of fluid flowing across C per unit time, or the rate of flow. This is analogous to using rectangles to approximate area in a single-variable integral. For a ,. First Order Differential Equations 2. Q: Evaluate the integral A:. Real Numbers Class Sequences 2. Problem 20RQ: Solve the problem, showing the details of your work. We have already examined the idea of components of force, in example