Exponential and logarithmic equation solver
Recall, for example.
Because Australia had few predators and ample food, the rabbit population exploded. In fewer than ten years, the rabbit population numbered in the millions. Uncontrolled population growth, as in the wild rabbits in Australia, can be modeled with exponential functions. Equations resulting from those exponential functions can be solved to analyze and make predictions about exponential growth. In this section, we will learn techniques for solving exponential functions.
Exponential and logarithmic equation solver
.
We can use this fact, along with the rules of logarithms, to solve logarithmic equations where the argument is an algebraic expression.
.
Recall, for example. With this interpretation of real exponents, all rules and theorems for exponents are valid for real-number exponents as well as rational ones. In addition to the rules for exponents presented earlier, several new properties are used in this chapter. These properties are generalized below. Proofs of the properties are not given here, as they require more advanced mathematics.
Exponential and logarithmic equation solver
If you missed this problem, review Example 6. In the section on logarithmic functions, we solved some equations by rewriting the equation in exponential form. Now that we have the properties of logarithms, we have additional methods we can use to solve logarithmic equations. To use this property, we must be certain that both sides of the equation are written with the same base. Remember that logarithms are defined only for positive real numbers. Check your results in the original equation.
Asiahorse
The loudness of sounds is measured in a uni! The x -axis is a horizontal asymptote. While any appropriate base b can be used to apply Properly 2. This constant occurs again and again in nature, in mathematics, in science, in engineering, and in finance. The steps may be reversed with some calculators. For any positive real numbers x and y , real number r , and any positive real number a, a! Common Base Method Sometimes the common base for an exponential equation is not explicitly shown. New Example. For Property b to hold, a must not equal 1 since, for example. Natural logarithms can be found with a calculator that has an In key. In a community with little diversity, H is close to 0. Therefore, we can solve many exponential equations by using the rules of exponents to rewrite each side as a power with the same base. The chart below shows several pairs of equivalent statements. Find some ordered pairs. For all real numbers y , and all positive numbers a and x , where a!
Because Australia had few predators and ample food, the rabbit population exploded. In fewer than ten years, the rabbit population numbered in the millions.
As Figure 5. Help Tutorial. Use the one-to-one property to set the exponents equal. Example 3. See your instruction booklet for details or ask your instructor for assistance. The second statement in the theorem will be useful in Sections 5. A decimal approximation for x can be found using a calculator:. Since half of 40 is 20 , replace y with 20 in the formula, and solve for t. When an exponential equation cannot be rewritten with a common base, solve by taking the logarithm of each side. Similarly, the half-life of a quantity that decays exponentially is the amount of time that it takes for any initial amount to decay to half its value. In working with logarithms, it is helpful to remember the following. With a calculator, enter 85 , press the In key, and read the result, 4. The y -axis is a vertical asymptote.

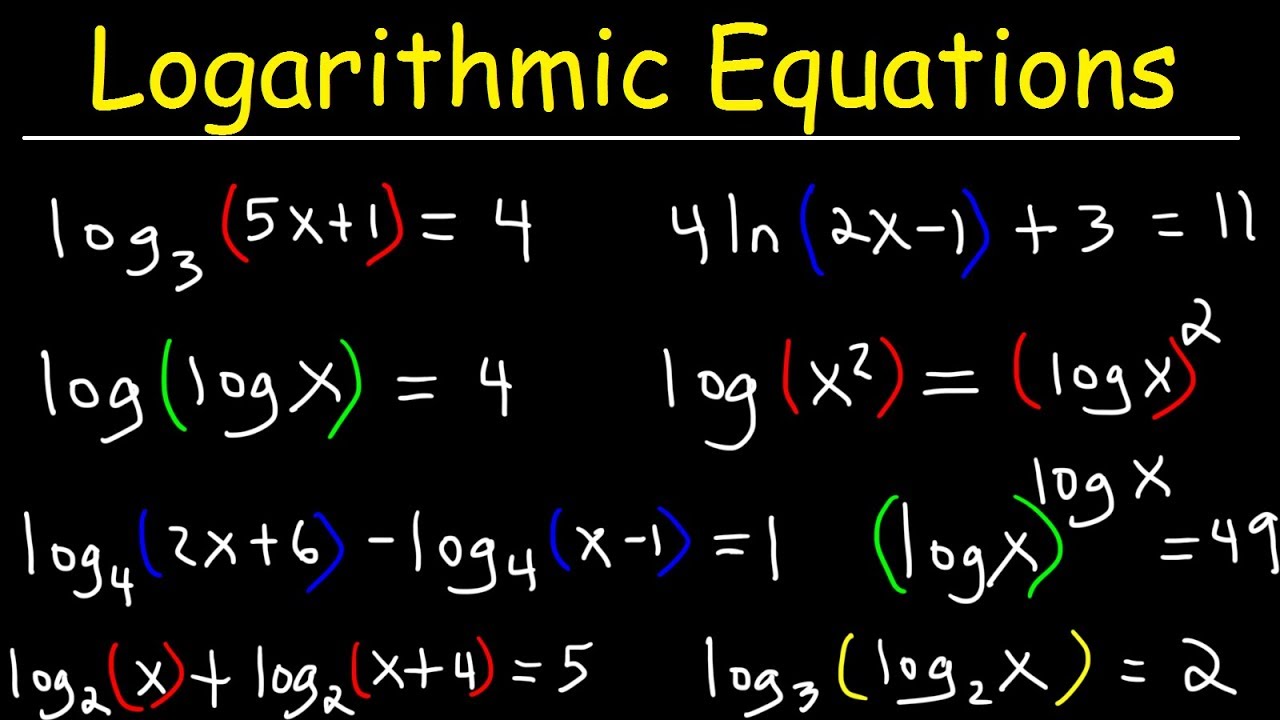
You have hit the mark. In it something is also to me it seems it is good idea. I agree with you.