Factor x 2 4
Solve Practice Play.
Does the sight of a number or expression accompanied by the instructions, "Factor completely," strike fear into your heart? Wish you paid attention in algebra? First off, what is a factor? For example, the number 5 has two factors: 1, and 5. The number 6 has four factors: 1, 2, 3, and 6.
Factor x 2 4
If you don't see it, please check your spam folder. Sometimes it can end up there. By signing up you agree to our terms and privacy policy. Subscribe now. Sign up for your FREE 7-day trial. Already have an account? Log in. Your Email. Get Annual Plans at a discount when you buy 2 or more! Your Plan. SparkNotes Plus. You'll be billed after your free trial ends. Not Applicable. Renews March 22, March 15, Discounts applied to next billing.
Then substitute it in by dividing the terms in the original expression by n. Payment Details. Over the rational numbers, it is possible to find polynomials, with degree as large as we like, that are irreducible.
The student should begin this chapter with a review of the idea of factoring integers. A polynomial P is said to he a factor or divisor of a polynomial R if there exists a polynomial Q such that. Note that Q is also a divisor of R. In this chapter we will agree that our polynomials are to have only integral coefficients. For example,. But, even though.
In multiplication, factors are the integers that are multiplied together to find other integers. In this example, 6 and 5 are the factors of Essentially, an integer a is a factor of another integer b , so long as b can be divided by a with no remainder. Factors are important when working with fractions, as well as when trying to find patterns within numbers. Prime factorization involves finding the prime numbers that, when multiplied, return the number being addressed. It can be helpful to use a factor tree when computing the prime factorizations of numbers. Using From the simple example of , it is clear that prime factorization can become quite tedious fairly quickly. Unfortunately, there is currently no known algorithm for prime factorization that is efficient for very large numbers.
Factor x 2 4
We have seen that some binomials and trinomials result from special products—squaring binomials and multiplying conjugates. If you learn to recognize these kinds of polynomials, you can use the special products patterns to factor them much more quickly. Some trinomials are perfect squares. They result from multiplying a binomial times itself. We squared a binomial using the Binomial Squares pattern in a previous chapter. In this chapter, you will start with a perfect square trinomial and factor it into its prime factors. But if you recognize that the first and last terms are squares and the trinomial fits the perfect square trinomials pattern, you will save yourself a lot of work.
Lion king live action meme
These identities are generally covered in senior mathematics and are useful in beginning calculus and for finding limits. It was Gauss who first gave a proof that polynomials can be completely factored into linear factors over the complex numbers. We notice that the coefficient x of is the sum of the two numbers 2 and 5 in the brackets and that the constant term 10, is the product of 2 and 5. And no, I don't mean factoring the expression of your boss as you tell him you accidentally flooded the break room with coffee. Does the sight of a number or expression accompanied by the instructions, "Factor completely," strike fear into your heart? These identities are called the difference of cubes and sum of cubes respectively. Algebra Calculator. The highest common factor of the three terms is 2 ab so. Clearly the solutions are 4 and 3 in either order , and no other numbers satisfy these equations. Don't you think this expression would be easier to factor with smaller numbers and variable powers? Password Your password must: Be between characters. A polynomial is said to be factored completely when it is expressed as a product of prime factors.
Wolfram Alpha is a great tool for factoring, expanding or simplifying polynomials. It also multiplies, divides and finds the greatest common divisors of pairs of polynomials; determines values of polynomial roots; plots polynomials; finds partial fraction decompositions; and more.
The free trial period is the first 7 days of your subscription. You can say that a negative 4x is being added to 2x 2. A lone variable is raised to a power of one. We should always be on the look out for common factors before using other factoring techniques. Complete Purchase. Proficiency with algebra is an essential tool in understanding and being confident with mathematics. Basically, if you list all the factors of the constant, and divide them by the factors of the leading coefficient the coefficient next to the variable with the highest power in every combination, you will get a list of possible rational solutions. It also links in with the techniques discussed above. We will now apply the various techniques of factoring to simplify various algebraic expressions. Last Name. Note the solution, 4.

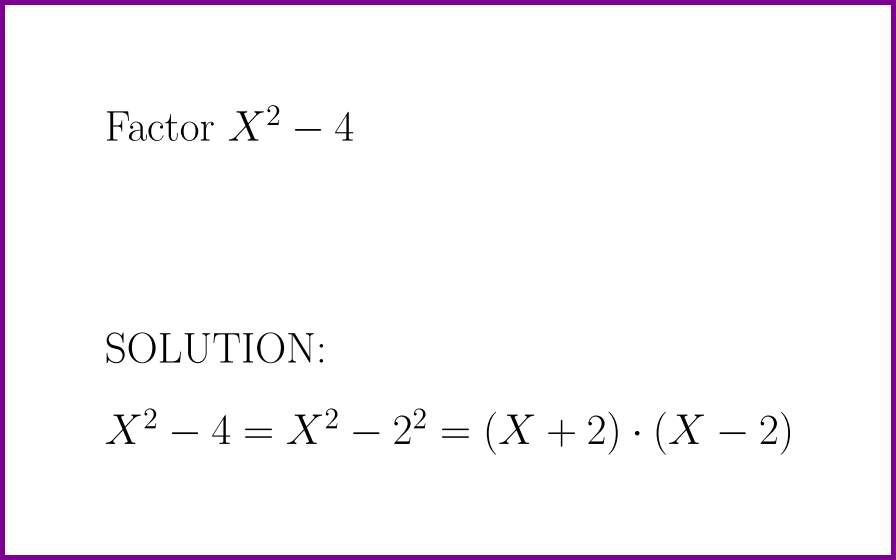
0 thoughts on “Factor x 2 4”