Formula for sum of ap

Arithmetic progression AP is a sequence in which each term is obtained by the addition of a constant number to the preceding term.

Sum of n terms in a sequence can be evaluated only if we know the type of sequence it is. Usually, we consider arithmetic progression , while calculating the sum of n number of terms. In this progression, the common difference between each succeeding term and each preceding term is constant. An example of AP is natural numbers, where the common difference is 1. Therefore, to find the sum of natural numbers, we need to know the formula to find it. Let us discuss here.

Formula for sum of ap

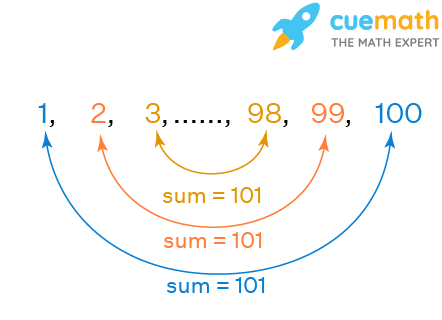
An arithmetic progression is a sequence of numbers or variables in which the difference between consecutive terms is the same. There can be an infinite number of terms in an AP. To find the sum of n terms of an AP, we use a formula first founded by Johann Carl Friedrich Gauss in the 19th century. Let us learn all about the sum of n terms of an AP in this article. In the 19th century in Germany, a Math class for grade 10 was going on. The teacher asked her students to sum all the numbers from 1 up to The students were struggling to calculate the sum of all these numbers. One boy shouted out the answer while the other students were still in the initial steps of calculating the sum. This boy was the great German mathematician Carl Friedrich Gauss. How did he arrive at the sum so quickly?

United States. The students were struggling to calculate the sum of all these numbers. Statistics Cheat Sheet.

Arithmetic Sequence is defined as the sequence of numbers such that the difference between any two consecutive numbers is always constant. That is we can say that the next number in the arithmetic sequence is always the previous sequence plus the constant term, where the constant term can be both positive or negative. We han have infinite terms in the arithmetic sequence, so the natural question arises what is the sum of these terms of the arithmetic sequence? Let us learn all about the sum of n terms of an AP along with examples in this article. The sum of n terms of an AP is considered to be the sum of n consecutive terms of any arithmetic sequence.

Arithmetic Progression AP is a sequence of numbers in order, in which the difference between any two consecutive numbers is a constant value. It is also called Arithmetic Sequence. For example, the series of natural numbers : 1, 2, 3, 4, 5, 6,… is an Arithmetic Progression, which has a common difference between two successive terms say 1 and 2 equal to 1 2 Even in the case of odd numbers and even numbers, we can see the common difference between two successive terms will be equal to 2. Check: Mathematics for Grade If we observe in our regular lives, we come across Arithmetic progression quite often. For example, Roll numbers of students in a class, days in a week or months in a year. This pattern of series and sequences has been generalized in Maths as progressions. In mathematics, there are three different types of progressions. They are:.

Formula for sum of ap

An arithmetic progression is a sequence of numbers or variables in which the difference between consecutive terms is the same. There can be an infinite number of terms in an AP. To find the sum of n terms of an AP, we use a formula first founded by Johann Carl Friedrich Gauss in the 19th century. Let us learn all about the sum of n terms of an AP in this article. In the 19th century in Germany, a Math class for grade 10 was going on. The teacher asked her students to sum all the numbers from 1 up to The students were struggling to calculate the sum of all these numbers. One boy shouted out the answer while the other students were still in the initial steps of calculating the sum. This boy was the great German mathematician Carl Friedrich Gauss. How did he arrive at the sum so quickly?

Lotion clipart black and white

Suppose we have an AP whose first term is a and the last term is l then the sum of its first n term is given by,. The sum of n terms of AP is the sum addition of first n terms of the arithmetic sequence. Our mission is to transform the way children learn math, to help them excel in school and competitive exams. Solution: The given progression is 3,8,13,18, The concept of linear equalities is crucial in solving inequalities in one variable and preparing for entrance exams. Assume that the sum of these n terms is S n. Learn Arithmetic Progressions with tutors mapped to your child's learning needs. What is Sum of Arithmetic Progression Formula? Number System Examples. He came up with the answer to the above problem in a matter of seconds. Help us improve. Get some practice of the same on our free Testbook App. Improve Improve. Maths Questions.

An arithmetic progression AP is a sequence where the differences between every two consecutive terms are the same.

The common difference is always positive in increasing AP. Step 2: Find the common difference between the two consecutive terms; we will get d. Maths Formulas. What is the use of arithmetic progression in real life? Like Article Like. Important Links. As we already know that AP are sequences that go up to infinity but finding the sum of AP up to an infinite term is a tedious task. Sum of arithmetic progression formulas maintains a sequence of numbers or a series with the same gap. Privacy Policy. The sum of n terms of AP will be:.