Gauss jordan solver

In this section, we learn to solve systems of linear equations using a process called the Gauss-Jordan method. The process begins by first expressing the system as a matrix, and then reducing it to an equivalent system by simple row operations, gauss jordan solver.

Gauss-Jordan Elimination is an algorithm that can be used to solve systems of linear equations and to find the inverse of any invertible matrix. It relies upon three elementary row operations one can use on a matrix:. The purpose of Gauss-Jordan Elimination is to use the three elementary row operations to convert a matrix into reduced-row echelon form. A matrix is in reduced-row echelon form , also known as row canonical form , if the following conditions are satisfied:. Matrices A and B are in reduced-row echelon form, but matrices C and D are not. C is not in reduced-row echelon form because it violates conditions two and three. D is not in reduced-row echelon form because it violates condition four.

Gauss jordan solver

This online calculator will help you to solve a system of linear equations using Gauss-Jordan elimination. Using this online calculator, you will receive a detailed step-by-step solution to your problem, which will help you understand the algorithm how to solve system of linear equations by Gauss-Jordan elimination. Change the names of the variables in the system. You can input only integer numbers, decimals or fractions in this online calculator More in-depth information read at these rules. The number of equations in the system: 2 3 4 5 6 Change the names of the variables in the system. Try online calculators. Solving of equations. Solving of quadratic equations Solving of biquadratic equations Solving systems of linear equations by substitution Gaussian elimination calculator Linear equations calculator: Cramer's rule Linear equations calculator: Inverse matrix method Show all online calculators. Try to solve the exercises from the theme equations. Quadratic equations.

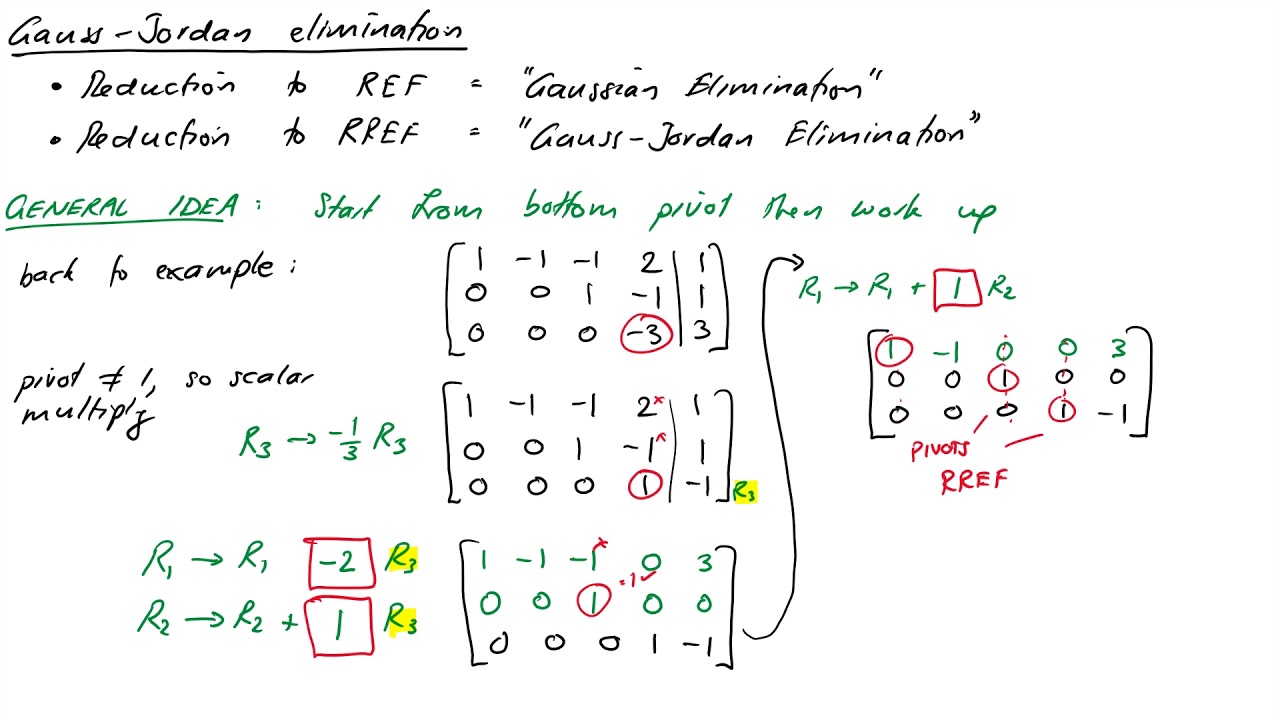
To make row 2, column 2 entry a 1, we divide the entire second row by —3. The process of obtaining a 1 in a location, and then making all other entries zeros in that column, is called pivoting, gauss jordan solver. Can I use the calculator to check my manual calculations?

We use cookies to improve your experience on our site and to show you relevant advertising. By browsing this website, you agree to our use of cookies. Learn more. Method 1. Adjoint 2. Gauss-Jordan Elimination 3. Cayley Hamilton Inverse of matrix using.

In mathematics, Gaussian elimination , also known as row reduction , is an algorithm for solving systems of linear equations. It consists of a sequence of row-wise operations performed on the corresponding matrix of coefficients. This method can also be used to compute the rank of a matrix, the determinant of a square matrix , and the inverse of an invertible matrix. The method is named after Carl Friedrich Gauss — To perform row reduction on a matrix, one uses a sequence of elementary row operations to modify the matrix until the lower left-hand corner of the matrix is filled with zeros, as much as possible. There are three types of elementary row operations:. Using these operations, a matrix can always be transformed into an upper triangular matrix , and in fact one that is in row echelon form. Once all of the leading coefficients the leftmost nonzero entry in each row are 1, and every column containing a leading coefficient has zeros elsewhere, the matrix is said to be in reduced row echelon form. This final form is unique; in other words, it is independent of the sequence of row operations used. For example, in the following sequence of row operations where two elementary operations on different rows are done at the first and third steps , the third and fourth matrices are the ones in row echelon form, and the final matrix is the unique reduced row echelon form.

Gauss jordan solver

In this section, we learn to solve systems of linear equations using a process called the Gauss-Jordan method. The process begins by first expressing the system as a matrix, and then reducing it to an equivalent system by simple row operations. The process is continued until the solution is obvious from the matrix. The matrix that represents the system is called the augmented matrix , and the arithmetic manipulation that is used to move from a system to a reduced equivalent system is called a row operation. We express the above information in matrix form. Since a system is entirely determined by its coefficient matrix and by its matrix of constant terms, the augmented matrix will include only the coefficient matrix and the constant matrix.

Score pak vs sri

The system of linear equations with 3 variables. Once a system is expressed as an augmented matrix, the Gauss-Jordan method reduces the system into a series of equivalent systems by using the row operations. Try to solve the exercises from the theme equations. The matrix that represents the system is called the augmented matrix , and the arithmetic manipulation that is used to move from a system to a reduced equivalent system is called a row operation. Applied Finite Mathematics Sekhon and Bloom. It relies upon three elementary row operations one can use on a matrix: Swap the positions of two of the rows Multiply one of the rows by a nonzero scalar. Since a system is entirely determined by its coefficient matrix and by its matrix of constant terms, the augmented matrix will include only the coefficient matrix and the constant matrix. Make sure you align your coefficients properly with the corresponding variables across the equations. Go back to previous article. Consider the system. The row to which a multiple of pivot row is added is called the target row. The system of linear equations with 4 variables. Calculation Click the "Calculate" button.

The Gauss-Jordan Elimination method is an algorithm to solve a linear system of equations.

Gauss-Jordan Elimination is an algorithm that can be used to solve systems of linear equations and to find the inverse of any invertible matrix. Can I use this calculator for any system of linear equations? One can easily see that these three row operation may make the system look different, but they do not change the solution of the system. Gauss Jacobi 7. If you encounter any issues or have additional queries, feel free to contact us. The method is not much different form the algebraic operations we employed in the elimination method in the first chapter. We get,. Learning Objectives In this section you will learn to Represent a system of linear equations as an augmented matrix Solve the system using elementary row operations. What's new. We need to make all other entries zeros in column 1. So far we have made a 1 in the left corner and all other entries zeros in that column. Matrix A : X. The second operation states that if a row is multiplied by any non-zero constant, the new system obtained has the same solution as the old one. The process of obtaining a 1 in a location, and then making all other entries zeros in that column, is called pivoting.