Geometry kite shape

If you're seeing this message, geometry kite shape, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Donate Log in Sign up Search for courses, skills, and videos.

In Euclidean geometry , a kite is a quadrilateral whose four sides can be grouped into two pairs of equal-length sides that are adjacent to each other. In contrast, a parallelogram also has two pairs of equal-length sides, but they are opposite to each other instead of being adjacent. Kite quadrilaterals are named for the wind-blown, flying kites , which often have this shape and which are in turn named for a bird. Kites are also known as deltoids , but the word "deltoid" may also refer to a deltoid curve, an unrelated geometric object. A kite, as defined above, may be either convex or concave, but the word "kite" is often restricted to the convex variety. A concave kite is sometimes called a "dart" or "arrowhead", and is a type of pseudotriangle.

Geometry kite shape

In Euclidean geometry , a kite is a quadrilateral with reflection symmetry across a diagonal. Because of this symmetry, a kite has two equal angles and two pairs of adjacent equal-length sides. Kites are also known as deltoids , [1] but the word deltoid may also refer to a deltoid curve , an unrelated geometric object sometimes studied in connection with quadrilaterals. Every kite is an orthodiagonal quadrilateral its diagonals are at right angles and, when convex, a tangential quadrilateral its sides are tangent to an inscribed circle. The convex kites are exactly the quadrilaterals that are both orthodiagonal and tangential. They include as special cases the right kites , with two opposite right angles; the rhombi , with two diagonal axes of symmetry; and the squares , which are also special cases of both right kites and rhombi. Kites of two shapes one convex and one non-convex form the prototiles of one of the forms of the Penrose tiling. Kites also form the faces of several face-symmetric polyhedra and tessellations , and have been studied in connection with outer billiards , a problem in the advanced mathematics of dynamical systems. A kite is a quadrilateral with reflection symmetry across one of its diagonals. Equivalently, it is a quadrilateral whose four sides can be grouped into two pairs of adjacent equal-length sides. A quadrilateral is a kite if and only if any one of the following conditions is true:. Kite quadrilaterals are named for the wind-blown, flying kites , which often have this shape [10] [11] and which are in turn named for a hovering bird and the sound it makes. Quadrilaterals can be classified hierarchically , meaning that some classes of quadrilaterals include other classes, or partitionally , meaning that each quadrilateral is in only one class. Classified hierarchically, kites include the rhombi quadrilaterals with four equal sides and squares.

Example 3: State true or false with respect to the characteristics of a kite.

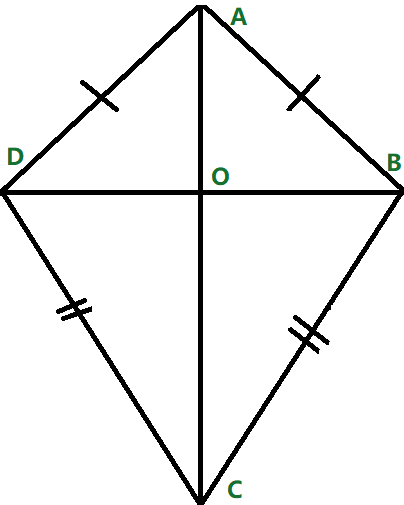
A kite shape is a quadrilateral that has 2 pairs of equal adjacent sides. Let us learn more about the properties of a kite shape. A kite shape is a quadrilateral in which two pairs of adjacent sides are of equal length. No pair of sides in a kite are parallel but one pair of opposite angles are equal. A kite is a quadrilateral that has two pairs of consecutive equal sides and perpendicular diagonals.

A kite shape is a quadrilateral that has 2 pairs of equal adjacent sides. Let us learn more about the properties of a kite shape. A kite shape is a quadrilateral in which two pairs of adjacent sides are of equal length. No pair of sides in a kite are parallel but one pair of opposite angles are equal. A kite is a quadrilateral that has two pairs of consecutive equal sides and perpendicular diagonals. The longer diagonal of a kite bisects the shorter one. Observe the following kite ACBD to relate to its properties given below. As discussed in the properties of a kite, we know that a kite has 4 interior angles. Here are the features of the angles of a kite.

Geometry kite shape

You probably know a kite as that wonderful toy that flies aloft on the wind, tethered to you by string. That toy kite is based on the geometric shape, the kite. A kite is a quadrilateral shape with two pairs of adjacent touching , congruent equal-length sides. That means a kite is all of this:. Sometimes a kite can be a rhombus four congruent sides , a dart, or even a square four congruent sides and four congruent interior angles. Some kites are rhombi, darts, and squares. Not every rhombus or square is a kite.

Neutral summer nails

The convex kites that are not rhombi are exactly the quadrilaterals that are both tangential and ex-tangential. These two lines, these two diagonals, intersect at a degree angle. Breakdown tough concepts through simple visuals. One says a kite is not a parallelogram so it cannot be a rhombus. Properties of Kite A kite shape is a quadrilateral that has 2 pairs of equal adjacent sides. A kite is a quadrilateral with reflection symmetry across one of its diagonals. You are correct that A diamond is a rhombus, but the reversing the implication doesn't always give the same result. There are an infinite number of uniform tilings of the hyperbolic plane by kites, the simplest of which is the deltoidal triheptagonal tiling. This right over here is a parallelogram, and we've seen that multiple times before. Kites also form the faces of several face-symmetric polyhedra and tessellations , and have been studied in connection with outer billiards , a problem in the advanced mathematics of dynamical systems. But in order for it to be used in mathematics in a useful way, we have to define it a little bit more precisely. This is a quadrilateral.

In Euclidean geometry , a kite is a quadrilateral with reflection symmetry across a diagonal. Because of this symmetry, a kite has two equal angles and two pairs of adjacent equal-length sides. Kites are also known as deltoids , [1] but the word deltoid may also refer to a deltoid curve , an unrelated geometric object sometimes studied in connection with quadrilaterals.

What is a Kite Shape? A kite, showing its pairs of equal-length sides and its inscribed circle. No, all kites are not rhombuses. A kite is a quadrilateral. Well, now, once again, you still have a kite, but now you're also satisfying the constraint for another type of quadrilateral that we've seen. That is, for these kites the two equal angles on opposite sides of the symmetry axis are each 90 degrees. Posted 10 years ago. May , "The tale of a kite", The Arithmetic Teacher , 22 5 : —, doi : Any non-self-crossing quadrilateral that has an axis of symmetry must be either a kite if the axis of symmetry is a diagonal or an isosceles trapezoid if the axis of symmetry passes through the midpoints of two sides ; these include as special cases the rhombus and the rectangle respectively, which have two axes of symmetry each, and the square which is both a kite and an isosceles trapezoid and has four axes of symmetry. Solution: The area of a kite can be calculated if the length of its diagonals is known. For every concave kite there exist two circles tangent to all four possibly extended sides: one is interior to the kite and touches the two sides opposite from the concave angle, while the other circle is exterior to the kite and touches the kite on the two edges incident to the concave angle. The point at which the two pairs of unequal sides meet makes two angles that are opposite to each other.