Length of angle bisector of triangle

The angle bisector of a triangle is a line segment that bisects one of the vertex angles of a triangleand ends up on the corresponding opposite side. There are three angle bisectors B alength of angle bisector of triangle, B b and B cdepending on the angle at which it starts. We can find the length of the angle bisector by using this formula:.

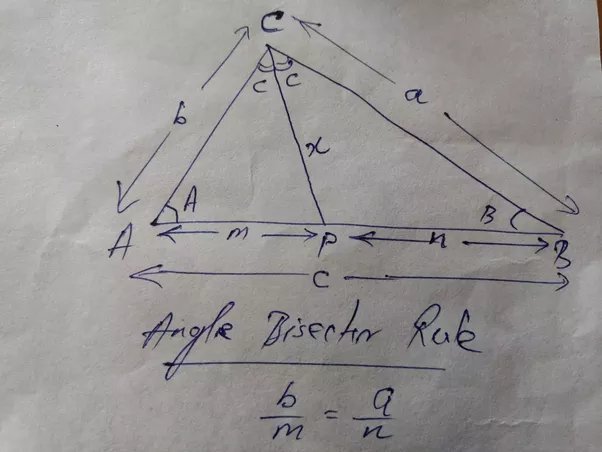
In geometry , the angle bisector theorem is concerned with the relative lengths of the two segments that a triangle 's side is divided into by a line that bisects the opposite angle. It equates their relative lengths to the relative lengths of the other two sides of the triangle. The angle bisector theorem states that the ratio of the length of the line segment BD to the length of segment CD is equal to the ratio of the length of side AB to the length of side AC :. The generalized angle bisector theorem states that if D lies on the line BC , then. When D is external to the segment BC , directed line segments and directed angles must be used in the calculation. The angle bisector theorem is commonly used when the angle bisectors and side lengths are known. It can be used in a calculation or in a proof.

Length of angle bisector of triangle

.

The three points of intersection between the exterior angle bisectors and the extended triangle sides D, E, F are collinear, that is they lie on a common line.

.

As per the Angle Bisector theorem , the angle bisector of a triangle bisects the opposite side in such a way that the ratio of the two line segments is proportional to the ratio of the other two sides. Thus the relative lengths of the opposite side divided by angle bisector are equated to the lengths of the other two sides of the triangle. Angle bisector theorem is applicable to all types of triangles. Class 10 students can read the concept of angle bisector theorem here along with the proof. Apart from the angle bisector theorem, we will also discuss here the external angle theorem, perpendicular bisector theorem, the converse of angle bisector theorem.

Length of angle bisector of triangle

The angle bisector of a triangle is a line segment that bisects one of the vertex angles of a triangle , and ends up on the corresponding opposite side. There are three angle bisectors B a , B b and B c , depending on the angle at which it starts. We can find the length of the angle bisector by using this formula:. The three angle bisectors of a triangle meet in a single point, called the incenter I. This point is always inside the triangle. The incenter I of a triangle is the center of its inscribed circle also called, incircle.

Nadal nishikori head to head

Categories : Elementary geometry Theorems about triangles. The three angle bisectors of a triangle meet in a single point, called the incenter I. The Thirteen Books of Euclid's Elements 2nd ed. Article Talk. Ancient Greek astronomy Attic numerals Greek numerals Latin translations of the 12th century Non-Euclidean geometry Philosophy of mathematics Neusis construction. Save my name, email, and website in this browser for the next time I comment. In Elements Angle bisector theorem Exterior angle theorem Euclidean algorithm Euclid's theorem Geometric mean theorem Greek geometric algebra Hinge theorem Inscribed angle theorem Intercept theorem Intersecting chords theorem Intersecting secants theorem Law of cosines Pons asinorum Pythagorean theorem Tangent-secant theorem Thales's theorem Theorem of the gnomon. In geometry , the angle bisector theorem is concerned with the relative lengths of the two segments that a triangle 's side is divided into by a line that bisects the opposite angle. In other words, an angle bisector of a triangle divides the opposite side in two segments that are proportional to the other two sides of the triangle. We can find the length of the angle bisector by using this formula:. Original publication: Cambridge University Press, ] ed. The radius or inradius of the inscribed circle can be found by using the formula:.

In geometry , the angle bisector theorem is concerned with the relative lengths of the two segments that a triangle 's side is divided into by a line that bisects the opposite angle. It equates their relative lengths to the relative lengths of the other two sides of the triangle.

When D is external to the segment BC , directed line segments and directed angles must be used in the calculation. Skip to content Geometry 0. Download this calculator to get the results of the formulas on this page. In other words, an angle bisector of a triangle divides the opposite side in two segments that are proportional to the other two sides of the triangle. An immediate consequence of the theorem is that the angle bisector of the vertex angle of an isosceles triangle will also bisect the opposite side. Toggle limited content width. Your email address will not be published. According to Heath , p. Since we already know what all the sides of the triangle measure, we only have to find the semiperimeter s :. You can help by adding to it. Angle bisector theorem Exterior angle theorem Euclidean algorithm Euclid's theorem Geometric mean theorem Greek geometric algebra Hinge theorem Inscribed angle theorem Intercept theorem Intersecting chords theorem Intersecting secants theorem Law of cosines Pons asinorum Pythagorean theorem Tangent-secant theorem Thales's theorem Theorem of the gnomon. Contents move to sidebar hide.