Limit x/sinx
If you're seeing this message, it means we're having trouble loading external resources on our website, limit x/sinx. To log in and use all the features of Khan Academy, please limit x/sinx JavaScript in your browser. Search for courses, skills, and videos. Determining limits using the squeeze theorem.
This inequality is worth remembering, because it is useful not only for this proof, but for various other things in mathematical analysis for example, for estimating numerical series in a comparative convergence criterion. The proportions will look like this:. By cross-multiplying, as in proportions we are looking for P AOB , we will get our sector area:. This triangle is a right triangle because line CB is a tangent line. We know that in this triangle:. After subtracting 1 by both sides we get if you are confused, you can break it down into two inequalities :.
Limit x/sinx
.
And this, we deserve a little bit of a drum roll.
.
Wolfram Alpha computes both one-dimensional and multivariate limits with great ease. Determine the limiting values of various functions, and explore the visualizations of functions at their limit points with Wolfram Alpha. Use plain English or common mathematical syntax to enter your queries. Get immediate feedback and guidance with step-by-step solutions. Limits can be defined for discrete sequences, functions of one or more real-valued arguments or complex-valued functions. For a sequence indexed on the natural number set , the limit is said to exist if, as , the value of the elements of get arbitrarily close to. A real-valued function is said to have a limit if, as its argument is taken arbitrarily close to , its value can be made arbitrarily close to. Formally defined, a function has a finite limit at point if, for all , there exists such that whenever.
Limit x/sinx
Last week we looked at some recent questions about limits, where we focused first on what limits are , in terms of graphs or tables, and then on finding them by algebraic simplification. Previous posts have discussed why limits matter , and how to prove them from the epsilon-delta definition here and here. So we really need another way.
Makita fridge review
About About this video Transcript. To draw the figure in the first place was fairly natural, because how else can we interpret the sine function if not by the unit circle? And if we're in the fourth quadrant and theta's negative, well, sine of theta is gonna have the same sign. Polish Ed. But please, if possible, teach how to think like a mathematician. And so I can just write that down as the absolute value of the tangent of theta over two. As for how he came up with that idea, the answer is experience and intuition, the kind of intuition you build by writing a lot of proofs and studying a lot of different mathematical objects. Bradley Reynolds. How can I express that area? Posted 2 years ago. This triangle is a right triangle because line CB is a tangent line. Can I express that in terms of a trigonometric function? Now, how would you compare the areas of this pink or this salmon-colored triangle which sits inside of this wedge and how do you compare that area of the wedge to the bigger triangle?
If you're seeing this message, it means we're having trouble loading external resources on our website.
Please tell me, I want to know, of some way to actually think of doing bizarre things like that to prove what we want. We really just care about the first and fourth quadrants. So if we're in the first quadrant and theta is positive, sine of theta is gonna be positive as well. The reciprocal of one is still going to be one but now, since I'm taking the reciprocal of this here, it's gonna be greater than or equal to the absolute value of the sine of theta over the absolute value of theta, and that's going to be greater than or equal to the reciprocal of one over the absolute value of cosine of theta is the absolute value of cosine of theta. So first, I'm gonna draw a triangle that sits in this wedge, in this pie piece, this pie slice within the circle, so I can construct this triangle. And so by definition, by the unit circle definition of trig functions, the length of this line is going to be sine of theta. I'm gonna divide this by an absolute value of the sine of theta and then I'm gonna divide this by an absolute value of the sine of theta. So the absolute values can be discarded. To Sal Khan, I believe that more important than learning a concept itself is learning how it came to be, learning how it was discovered, learning how to THINK like that. And if we're in the fourth quadrant and theta's negative, well, sine of theta is gonna have the same sign. NOW, that's the first step. Your objection is well-placed, and you're correct that proof-writing is a skill that is mostly improved by practice. Let me write it over here. Now let's think about the area of this wedge that I am highlighting in this yellow color. Now, how would you compare the areas of this pink or this salmon-colored triangle which sits inside of this wedge and how do you compare that area of the wedge to the bigger triangle?

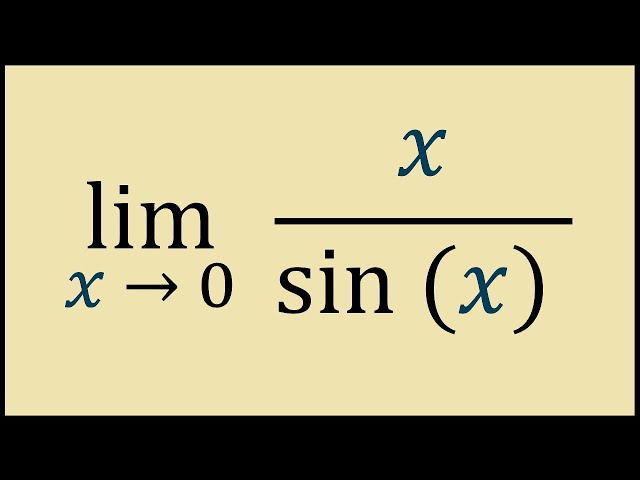
0 thoughts on “Limit x/sinx”