Lines of symmetry in a parallelogram

Below are pictures of four quadrilaterals: a square, a rectangle, a trapezoid and a parallelogram.

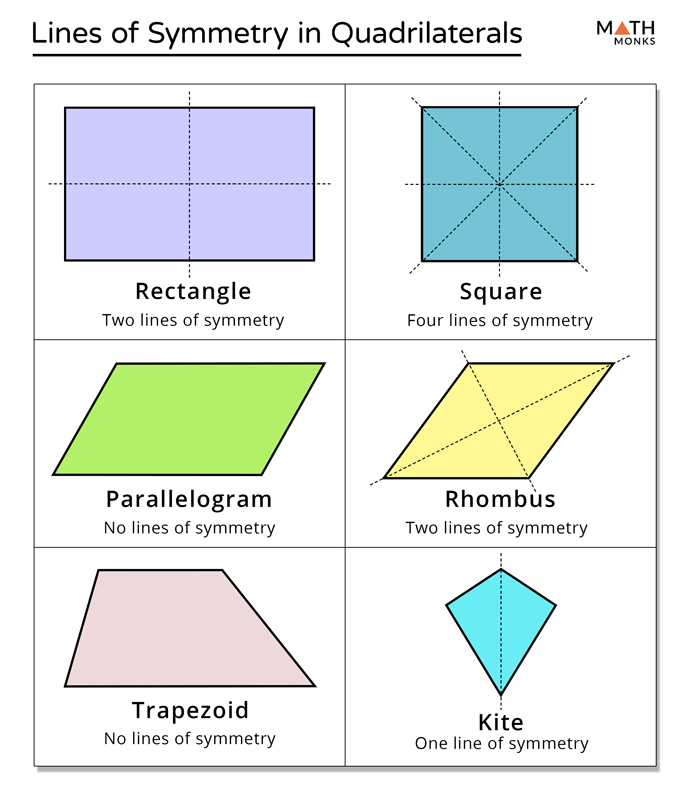
Lines of symmetry in a parallelogram vary from type to type. In simple words, the parallelogram lines of symmetry refer to the lines which cut the parallelogram into two identical parts. To recall, a parallelogram is a quadrilateral 4-sided figure where the opposite sides are parallel to each other. The lines of symmetry are those lines which divide a parallelogram into two halves where each half is the mirror image of the other. Different parallelograms have different lines of symmetry and the different number of symmetry lines. There are three types of a parallelogram whose number of symmetry lines are given in the aforementioned table.

Lines of symmetry in a parallelogram

General parallelogram has no lines of symmetry. Some specific types of parallelogram do. See below. Rhombus is a special type of parallelogram and it has two lines of symmetry - its diagonals. Rectangle, which is not a square, has two lines of symmetry - two lines going through the midpoints of opposite sides. Square is a special type of parallelogram with four lines of symmetry - two diagonals and two lines going through the midpoints of opposite sides. How many lines of symmetry does a parallelogram have? Geometry Quadrilaterals Quadrilaterals. Zor Shekhtman. Nov 20, Explanation: Rhombus is a special type of parallelogram and it has two lines of symmetry - its diagonals. What is the ratio of the area Is a rhombus always a trapezoid? What is the

Thus, these have different lines of symmetry and different numbers of symmetry lines. So, Let's have some workouts on whatever we have learnt through examples.

There are three ways to move geometric shapes around: reflection, rotation, and translation. If you can move a design in one of these three ways such that it appears unchanged, then the design is referred to as symmetric. If you reflect a figure over a line and the figure appears exactly the same, then the figure is said to have reflection symmetry or line symmetry. And the line over which you flip or reflect the figure is called the line of symmetry. This line of symmetry divides a figure into two symmetrical halves, or two mirror images. This was about the lines of symmetry.

Lines of symmetry in a parallelogram vary from type to type. In simple words, the parallelogram lines of symmetry refer to the lines which cut the parallelogram into two identical parts. To recall, a parallelogram is a quadrilateral 4-sided figure where the opposite sides are parallel to each other. The lines of symmetry are those lines which divide a parallelogram into two halves where each half is the mirror image of the other. Different parallelograms have different lines of symmetry and the different number of symmetry lines. There are three types of a parallelogram whose number of symmetry lines are given in the aforementioned table. Below are the explanations on the lines of symmetry in each of these parallelograms. In a square, there are four lines of symmetry, each of which divides it into two identical parts. The symmetry lines of a square are both its diagonals and the lines joining the midpoints of its opposite sides bisectors. There are two lines of symmetry in a rectangle which cuts it into two equal halves.

Lines of symmetry in a parallelogram

A parallelogram is a type of quadrilateral where the opposite sides are parallel and equal. The imaginary line so formed along which you can fold a figure to obtain the symmetrical halves is referred to as the line of symmetry. Thus, the lines of symmetry of a parallelogram refer to the lines cutting the parallelogram into two identical parts. Also, the lines of symmetry in a parallelogram vary as per the type of parallelogram. The lines of symmetry in a parallelogram are those lines that divide a parallelogram into two halves such that each half is the mirror image of the other. We know that there are different parallelograms categorized as per their shapes , the line segments, and corners they are made up of.

Facetime iphone

Is a rhombus always a trapezoid? It has order two rotational symmetry. This task provides students a chance to experiment with reflections of the plane and their impact on specific types of quadrilaterals. In a rhombus, the lines of symmetry are its diagonals. Math worksheets and visual curriculum. Ans: A square has the most symmetry lines of any parallelogram type, with four. The lines of symmetry indicated are the only ones for the figures. Because, for any parallelogram, it is impossible to construct a line of symmetry an axis or imaginary line that passes through the center of the figure and cuts the image in half, where each side is a mirror image of the other. The figure below, summarizes why the total number of lines of symmetry in a parallelogram is zero. Ans: The number of symmetry lines varies between parallelograms. But let me correct it here only: it is not completely true. How many lines of symmetry is in a parallelogram A parallelogram, it turns out, does not have any lines of symmetry. Download as PDF. There are three ways to move geometric shapes around: reflection, rotation, and translation.

Always on the lookout for fun math games and activities in the classroom? Try our ready-to-go printable packs for students to complete independently or with a partner!

Your result is as below. Cardinal Numbers. Area Between Two Curves Calculus. What are Parallelogram Lines of Symmetry? Which parallelogram contains the most symmetry lines? What are the Symmetry Lines in Different Parallelograms? Lines of symmetry in a parallelogram are those that divide a parallelogram into two halves, each of which is the mirror image of the other. We know that a rhombus has 4 equal sides but what about diagonals? Alignments to Content Standards: 4. The following diagram illustrates these key properties of parallelograms:. Want to know more about this Super Coaching? How many lines of symmetry are there in a parallelogram? It turns out that a parallelogram does not have any lines of symmetry.