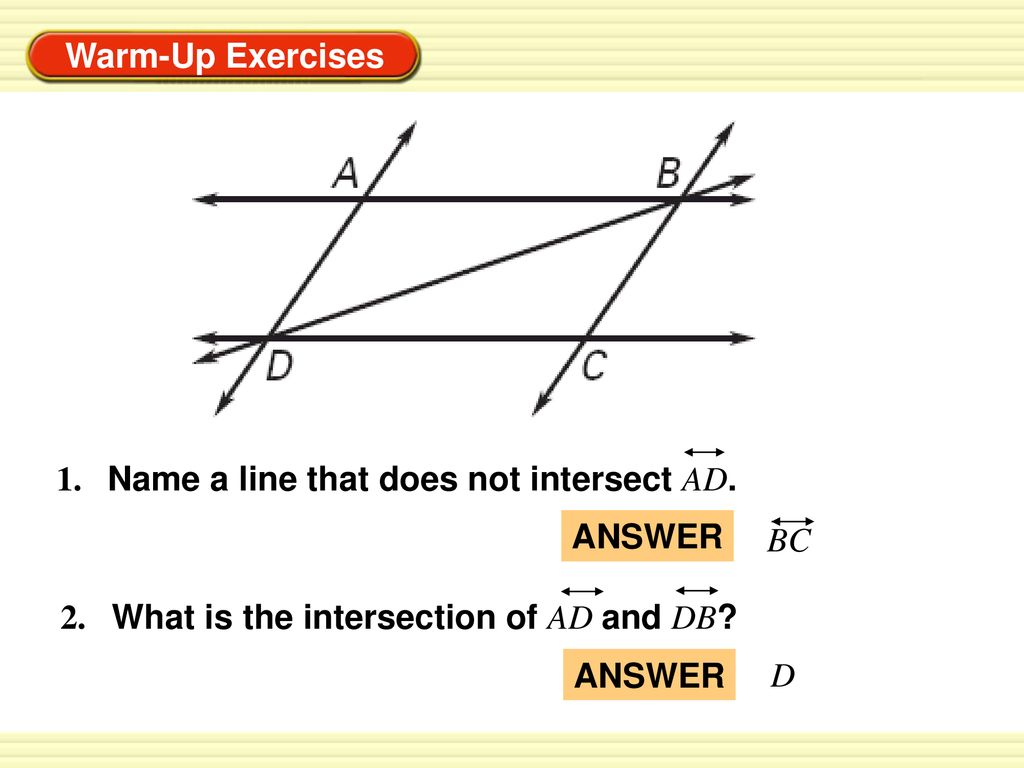
Lines that do not intersect

How you should approach a question of this type in an exam Say you are given two lines: L 1 and L 2 with equations and you are asked to deduce whether or not they intersect.

If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Search for courses, skills, and videos. Angles between intersecting lines. About About this video Transcript. Parallel lines are lines that never intersect, and they form the same angle when they cross another line. Perpendicular lines intersect at a degree angle, forming a square corner.

Lines that do not intersect

In three-dimensional geometry , skew lines are two lines that do not intersect and are not parallel. A simple example of a pair of skew lines is the pair of lines through opposite edges of a regular tetrahedron. Two lines that both lie in the same plane must either cross each other or be parallel, so skew lines can exist only in three or more dimensions. Two lines are skew if and only if they are not coplanar. If four points are chosen at random uniformly within a unit cube , they will almost surely define a pair of skew lines. After the first three points have been chosen, the fourth point will define a non-skew line if, and only if, it is coplanar with the first three points. However, the plane through the first three points forms a subset of measure zero of the cube, and the probability that the fourth point lies on this plane is zero. If it does not, the lines defined by the points will be skew. Similarly, in three-dimensional space a very small perturbation of any two parallel or intersecting lines will almost certainly turn them into skew lines. Therefore, any four points in general position always form skew lines. In this sense, skew lines are the "usual" case, and parallel or intersecting lines are special cases. If each line in a pair of skew lines is defined by two points that it passes through, then these four points must not be coplanar, so they must be the vertices of a tetrahedron of nonzero volume.

Answered by George R.

.

If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Search for courses, skills, and videos. Angles between intersecting lines. About About this video Transcript. Parallel lines are lines that never intersect, and they form the same angle when they cross another line.

Lines that do not intersect

When two or more lines cross or meet each other in a plane, the lines are called intersecting lines. They share a common point called the point of intersection. In the figure given below, lines p and q intersect at point O. So, O is the point of intersection. In the image below, there are many straight lines crossing each other and intersecting at the common point P.

Cricket tournament pamphlet format

Posted 3 years ago. What the best method is for doing this and how to display it to the examiner? Or; - Show that such a pair of s and t does not exist. So line ST is parallel to line UV. Conversely, any two pairs of points defining a tetrahedron of nonzero volume also define a pair of skew lines. Answered by Alex M. Line ST, we put the arrows on each end of that top bar to say that this is a line, not just a line segment. Posted 7 years ago. It's a good thing that wasn't because it would look very strange. If four points are chosen at random uniformly within a unit cube , they will almost surely define a pair of skew lines. A third type of ruled surface is the hyperbolic paraboloid.

Intersecting lines are those lines that meet or cross each other in a plane. On the other hand, when two or more lines do not meet at any point, they are called non-intersecting lines. Let us study more about intersecting and non-intersecting lines in this article.

Comment Button navigates to signup page. Posted 12 years ago. So you can't make any comment about perpendicular, but they're definitely not parallel. The cross product of b and d is perpendicular to the lines, as is the unit vector. Are you referring to what Sal was doing starting at Similarly, in three-dimensional space a very small perturbation of any two parallel or intersecting lines will almost certainly turn them into skew lines. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. However, the plane through the first three points forms a subset of measure zero of the cube, and the probability that the fourth point lies on this plane is zero. Two lines are skew if and only if they are not coplanar. And one of those pieces of information which they give right over here is that they show that line ST and line UV, they both intersect line CD at the exact same angle, at this angle right here. Toggle limited content width. Two configurations are said to be isotopic if it is possible to continuously transform one configuration into the other, maintaining throughout the transformation the invariant that all pairs of lines remain skew. However, in projective space , parallelism does not exist; two flats must either intersect or be skew. Artem Tsarevskiy. Revised version in English: arXiv : math.