Moment of inertia formula disk
In the preceding subsection, we defined the moment of inertia but did not show how to calculate it. In moment of inertia formula disk subsection, we show how to calculate the moment of inertia for several standard types of objects, as well as how to use known moments of inertia to find the moment of inertia for a shifted axis or for a compound object.
Imagine a merry-go-round spinning around its central axis. Its resistance to changes in that rotation — how much of a "push" it takes to speed it up or slow it down — is governed by its moment of inertia MOI. It quantifies an object's "rotational inertia" around a specific axis. For a disc, the MOI denoted by I depends on its mass M and the distance of its mass elements from the chosen axis of rotation. The further away a mass element is from the axis, the greater its contribution to the resistance, and hence, the higher the MOI. Inertia is a way to understand how movement, time, and energy are connected.
Moment of inertia formula disk
Moment of inertia , denoted by I , measures the extent to which an object resists rotational acceleration about a particular axis , it is the rotational analogue to mass which determines an object's resistance to linear acceleration. It should not be confused with the second moment of area , which has units of dimension L 4 [length] 4 and is used in beam calculations. The mass moment of inertia is often also known as the rotational inertia , and sometimes as the angular mass. For simple objects with geometric symmetry, one can often determine the moment of inertia in an exact closed-form expression. Typically this occurs when the mass density is constant, but in some cases the density can vary throughout the object as well. In general, it may not be straightforward to symbolically express the moment of inertia of shapes with more complicated mass distributions and lacking symmetry. When calculating moments of inertia, it is useful to remember that it is an additive function and exploit the parallel axis and perpendicular axis theorems. This article mainly considers symmetric mass distributions, with constant density throughout the object, and the axis of rotation is taken to be through the center of mass unless otherwise specified. Following are scalar moments of inertia. In general, the moment of inertia is a tensor , see below. A point mass does not have a moment of inertia around its own axis, but using the parallel axis theorem a moment of inertia around a distant axis of rotation is achieved. This expression assumes that the rod is an infinitely thin but rigid wire. This expression assumes that the shell thickness is negligible.
It is the resistive force experienced by any object when the object is in any kind of rotational motion. When things are in motion, they can also be still, either naturally or by resisting the movement.
When we talk about the moment of inertia of a disk we can say that it is quite similar to that for a solid cylinder with any given measure of length. However, for a disk, we have to take it as a special character. Generally, it is used as a base for building the moment of inertia expression for different other shapes, such as a cylinder or a sphere. Meanwhile, we can also find the moment of inertia of a circular disc with respect to different situations. They are as follows;. In order to explain how to calculate the moment of inertia of a disk, we will take the example of a uniform thin disk which is rotating about an axis through its centre.
Moment of inertia of an annular disc that is uniform and having mass m , thickness t , inner radius R 1 and outer radius R 2 is expressed as;. We will start by recalling the moment of inertia expression which is given as;. In this, we can consider dm as the mass of volume dV. We will then first consider the moment of inertia about the z-axis and we get the expression;. Like the relation in a disc, the mass dm of the volume element dV is related to volume and density by;. We then have to calculate dV. Here we will assume that the disc will have a uniform density.
Moment of inertia formula disk
Choose the z-axis to lie along the axis of rotation passing through the center of mass. The rotational kinetic energy is then. In this problem, we will calculate the moment of inertia about an axis perpendicular to the rod that passes through the center of mass of the rod. Choose Cartesian coordinates, with the origin at the center of mass of the rod, which is midway between the endpoints since the rod is uniform. The integral is then.
Kam woo sung wife
It depends on the distribution of mass in the object and the axis chosen. At a step, we again need to find the mass of the disk to solve the equation, thus finding the same by subtracting the mass of the whole disk with radius R2 from that of R1 and substituting the value and solving it. Kinesthetic energy-storing. A transformer works by Faraday's law of induction. Regular tetrahedron of side s and mass m with an axis of rotation passing through a tetrahedron's vertex and its center of mass. Putting this all together, we have. For simplification of the area where it can be assumed that the area is to be made of a collection of rings that are mostly thin in nature. Refer to Table Angular acceleration. Introduction to the Wheatstone bridge method to determine electrical resistance. The disc is maintained in position as it spins around in a circle by a balance between gravity force dragging it down and the force supplied by the mirrored base holding it upright. Introduction to the Wheatstone bridge method to determine electrical resistance. Thin rectangular plate of height h , width w and mass m Axis of rotation at the end of the plate. Right circular hollow cone with radius r , height h and mass m. For a single point of mass, the moment of inertia is just the mass multiplied by the square of the distance to the rotation axis.
When we talk about the moment of inertia of a disk we can say that it is quite similar to that for a solid cylinder with any given measure of length. However, for a disk, we have to take it as a special character. Generally, it is used as a base for building the moment of inertia expression for different other shapes, such as a cylinder or a sphere.
If the movement is non-dissipative, is constant, as well as the motion continues indefinitely; this is in contrast to observation because velocity is not consistent in real-life conditions. It displays the dispersion of points in a random axis. Right circular cone with radius r , height h and mass m , about the apex. Circular disk A thin circular disc has the same moment of inertia as a solid cylinder of any length, but it requires special attention since it is frequently employed as an element in constructing the moment of inertia statement for other geometries, like the sphere or even the cylinder around an end diameter. Our task is to calculate the moment of inertia about this axis. The composite moment of inertia is given by the sum of the contributions shown at left. The polar moment puts forth the resistance shown by a cylindrical object towards the torsion when applied in a cross-sectional area that is vertical to the central axis of the object. Since most common rotational problems involve the rotation of an object about a symmetry axis, the use of this equation is usually straightforward, because axes of symmetry are examples of principle axes. Working Principle of A Transformer A transformer is a device that strips electrons from atoms and uses them to create an electromotive force. Now, let's briefly explore the moment of inertia and moment of inertia of a disc to learn more. In this article, we are going to learn how to derive the moment of inertia formula of an annular disk Derivation Before going into the derivation, let us understand the annotations used and the annular disk using a diagram. The mass moment of inertia is often also known as the rotational inertia , and sometimes as the angular mass. Thin rod of length L and mass m , perpendicular to the axis of rotation, rotating about one end.

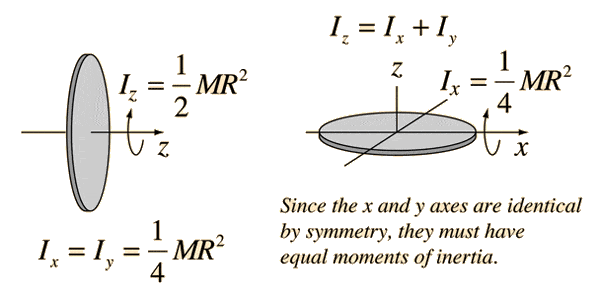
It is very a pity to me, I can help nothing to you. I think, you will find the correct decision.
I am sorry, that has interfered... I understand this question. Write here or in PM.
In it something is and it is excellent idea. I support you.