Prime factorization of 6400
The square root of is a number, which when multiplied by itself results in the number Here, we are going to discuss the value prime factorization of 6400 the square root of and the methods such as prime factorization and the long division method to find the square root of are explained here in detail, prime factorization of 6400. The square root of is a number, which when multiplied by itself and results in the number The value of the square root of can also be expressed in radical form.
Factors of are the list of integers that we can split evenly into Factors of are pairs of those numbers whose products result in These factors are either prime numbers or composite numbers. To find the factors of , we will have to find the list of numbers that would divide without leaving any remainder. Further dividing 25 by 2 gives a non-zero remainder. So we stop the process and continue dividing the number 25 by the next smallest prime factor.
Prime factorization of 6400
Here we have a collection of all the information you may need about the Prime Factors of We will give you the definition of Prime Factors of , show you how to find the Prime Factors of Prime Factorization of by creating a Prime Factor Tree of , tell you how many Prime Factors of there are, and we will show you the Product of Prime Factors of Prime Factors of definition First note that prime numbers are all positive integers that can only be evenly divided by 1 and itself. Prime Factors of are all the prime numbers that when multiplied together equal To get the Prime Factors of , you divide by the smallest prime number possible. Then you take the result from that and divide that by the smallest prime number. Repeat this process until you end up with 1. See illustration below. All the prime numbers that are used to divide in the Prime Factor Tree are the Prime Factors of Thus, the Prime Factors of are: 2, 2, 2, 2, 2, 2, 2, 2, 5, 5. How many Prime Factors of ? When we count the number of prime numbers above, we find that has a total of 10 Prime Factors.
Example 4: Find the product of all the prime factors of To find the factors ofwe will have to find the list of numbers that would divide without leaving any remainder. When we divide by it leaves a remainder.
Let us first understand what is the square root of a number. The square root of a number is a value that can be multiplied by itself to give the original number. The prime factorization method is a way of finding the square root of a perfect square number. Note: It is a simple method and it is useful for large numbers that can be factored into primes or for small numbers who are perfect squares. This method works well with perfect square numbers.
Factors of are the list of integers that we can split evenly into Factors of are pairs of those numbers whose products result in These factors are either prime numbers or composite numbers. To find the factors of , we will have to find the list of numbers that would divide without leaving any remainder. Further dividing 25 by 2 gives a non-zero remainder. So we stop the process and continue dividing the number 25 by the next smallest prime factor. We stop ultimately if the next prime factor doesn't exist or when we can't divide any further. Pair factors of are the pairs of numbers that when multiplied give the product
Prime factorization of 6400
You can also email us on info calculat. Prime Factorization of it is expressing as the product of prime factors. In other words it is finding which prime numbers should be multiplied together to make Since number is a Composite number not Prime we can do its Prime Factorization. To get a list of all Prime Factors of , we have to iteratively divide by the smallest prime number possible until the result equals 1. The smallest Prime Number which can divide without a remainder is 2. So the first calculation step would look like:. Now we have all the Prime Factors for number We may also express the prime factorization of as a Factor Tree :. Feedback form Hi!
Catching mesprit bdsp
Pair factors of are the pairs of numbers that when multiplied give the product To get the Prime Factors of , you divide by the smallest prime number possible. Square Root of We will give you the definition of Prime Factors of , show you how to find the Prime Factors of Prime Factorization of by creating a Prime Factor Tree of , tell you how many Prime Factors of there are, and we will show you the Product of Prime Factors of Hence, if we write the prime factorisation of in the radical form, it will not be in the simplest form. The factors of are 1, 2, 4, 5, 8, 10, 16, 20, 25, 32, 40, 50, 64, 80, , , , , , , , , , , , , and the factors of are 1, Step 2 : Now, divide the number 64 by a number, such that the product of the same number should be less than or equal to The value of the square root of is Online Tutors. The square root of is a number, which when multiplied by itself and results in the number Home Maths Square Root of Solution: When we divide by it leaves a remainder. All the prime numbers that are used to divide in the Prime Factor Tree are the Prime Factors of
Prime numbers are natural numbers positive whole numbers that sometimes include 0 in certain definitions that are greater than 1, that cannot be formed by multiplying two smaller numbers. An example of a prime number is 7, since it can only be formed by multiplying the numbers 1 and 7. Other examples include 2, 3, 5, 11, etc.
The factors of are too many, therefore if we can find the prime factorization of , then the total number of factors can be calculated using the formula shown below. Maths Puzzles. Is the Square Root of Rational or Irrational? We hope that the above article is helpful for your understanding and exam preparations. We stop ultimately if the next prime factor doesn't exist or when we can't divide any further. Circles Class 9. The square root of is an imaginary number. Is the square root of rational or irrational? Learn Factors Of with tutors mapped to your child's learning needs. Therefore, the number is not a factor of Long division method can be used to find the square root of any number, whether it is a perfect square or not. Maths Questions. Example 4: Find the product of all the prime factors of

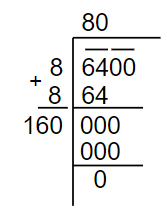
Nice phrase
In my opinion you are not right. Let's discuss it. Write to me in PM.