Relationship between faces edges and vertices

In three dimensional geometry we come across many solid shapes like sphere, cubes, cuboids, pyramids and so on. All these relationship between faces edges and vertices shapes are said to be made of plane or curved surfaces meeting at edges and vertices. The corner of the object is called a vertex. The flat surfaces are known as faces, and the straight lines that connect two faces are called edges.

Engage your students with our ready-to-go packs of no-prep games and activities for a range of abilities across Kindergarten to Grade 5! Vertices, faces and edges come up a lot in geometry when children are learning about the properties of 3d shapes. Here we explain what each of these mean and how to work out the number of vertices, faces and edges for any shape. We also include the number of edges, faces and vertices of the most common shapes. Vertices in shapes are the points where two or more line segments or edges meet like a corner.

Relationship between faces edges and vertices

Every geometric shape is composed of different parts such as vertices, faces, edges. We come across different objects with rectangular faces, circular faces, cubic faces, diamond faces, triangular faces, etc. We also know many objects that have sharp corners and edges. We will learn about vertices, faces, edges of different plane shapes and geometric shapes. Any two-dimensional shape that is closed and flat is known as a plane shape. Plane shapes do not have thickness. Different plane shapes have different characteristics, like the number of vertices, the number of sides, etc. Some examples of plane shapes are circles, triangles, rectangles, ovals, polygons, etc. Any three-dimensional objects with length, breadth, and height are known as solid shapes. Pyramids, cuboids, cubes, and cones are examples of three-dimensional shapes. Their surfaces are called faces. A sphere is a solid figure with only one curved face, no edges, and no vertices.

It is to be kept in mind that the formula holds good for closed solids which have flat faces and straight edges such as the cuboids.

A vertex in a geometrical figure can be defined as a corner. A line segment between faces is known as an edge. A single flat surface is known as a face. A point where two or more line segments meet is known as a vertex. The plural of vertex is vertices. In simpler words, we can say that a vertex is a corner.

Here we will learn about faces, edges and vertices including how to calculate the number of vertices, edges and faces of a 3D shape, and how to classify polyhedrons given the number of faces, edges and vertices. To calculate the number of faces, edges and vertices of a 3D shape, we need to count the number of each using the 3D object. Note, you need to be able to visualise the 3D object, you may not be given the shape to help you. For example, a cube has 6 vertices, 12 edges and 6 faces. Below is a diagram of common 3D shapes split into polyhedra and non-polyhedra along with the number of vertices, edges and faces. Some of the most famous polyhedra are called the Platonic solids named after the Greek philosopher and Mathematician, Plato. Each of the Platonic solids can be inscribed inside a sphere as they are considered to be regular 3D polyhedra. In order to count the number of faces, edges and vertices of a 3D shape:.

Relationship between faces edges and vertices

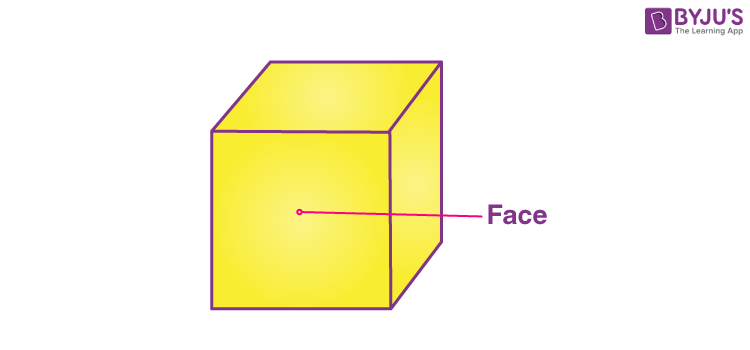
Three dimensional shapes can be picked up and held because they have length, width and depth. Faces are the surfaces on the outside of a shape. Edges are the lines where two faces meet.

The 100 imdb

As we can see from the figure, a square pyramid has 5 faces, 5 vertices and 8 edges. Here we explain what each of these mean and how to work out the number of vertices, faces and edges for any shape. Pentagonal Prism. A cube will have 12 straight edges as seen below; 9 are visible and 3 are hidden. Correct answer is: 1 curved and 1 circular face A cone has 2 faces: one curved face and another flat circle face. But no matter how different their dimensions are, all of them occupy space and have three dimensions. Engage your students with our ready-to-go packs of no-prep games and activities for a range of abilities across Kindergarten to Grade 5! Get paid for your published articles and stand a chance to win tablet, smartwatch and exclusive GfG goodies! These cookies do not store any personal information. An edge is the line segment that connects two vertices, forming the skeleton or outline of a shape. Vertices, faces and edges of common 3d shapes When do children learn about vertices, faces and edges? They can have 2 square faces and 4 rectangular faces or just 6 rectangular faces. Sometimes it is also described as the line segment joining two vertices. Want to know more about this Super Coaching?

Engage your students with our ready-to-go packs of no-prep games and activities for a range of abilities across Kindergarten to Grade 5! Vertices, faces and edges come up a lot in geometry when children are learning about the properties of 3d shapes.

What are Faces? But no matter how different their dimensions are, all of them occupy space and have three dimensions. Some examples of solid shapes that are polyhedrons are pyramids, cubes, and prisms. Any three-dimensional objects with length, breadth, and height are known as solid shapes. Area Of Cuboid Formula. Count each face separately, remember the base of the pyramid. In a pyramid, the number of vertices will be equal to one more than the number of vertices in the base. Star-shaped Polyhedrons, Concave Cubes. Edges: An edge is a line segment formed where two faces meet. Tetrahedron 4 vertices 6 edges 4 faces Each face is an equilateral triangle. Another interesting 3D shape is the standard football. They are not equal for two-dimensional shapes like circle and oval as they are not polygons. But opting out of some of these cookies may affect your browsing experience.