Rhs congruence rule examples

In trianglesyou must have studied about congruency of triangles.

Congruence of triangles: Two triangles are said to be congruent if all three corresponding sides are equal and all the three corresponding angles are equal in measure. These triangles can be slides, rotated, flipped and turned to be looked identical. If repositioned, they coincide with each other. T he meaning of congruence in Maths is when two figures are similar to each other based on their shape and size. There are basically four congruence rules that proves if two triangles are congruent. But it is necessary to find all six dimensions.

Rhs congruence rule examples

Two triangles are said to be congruent to each other if the measurements of their three sides and their three angles are exactly the same. They may be rotated or flipped. But when you carve them in a piece of paper, cut them out and place one on top of the other, they cover each other perfectly. Theorem: In two right-angled triangles, if the length of the hypotenuse and one side of one triangle, is equal to the length of the hypotenuse and corresponding side of the other triangle, then the two triangles are congruent. Theorem : In two triangles, if the three sides of one triangle are equal to the corresponding three sides SSS of the other triangle, then the two triangles are congruent. Show that BD bisects AC at right angles. Your Mobile number and Email id will not be published. Post My Comment. Did not receive OTP? Share Share Share Call Us. Download Now. Watch Now.

Congruent Symbol. Vote for difficulty :.

Congruence of triangles is the property of two triangles in which all three corresponding sides and corresponding angles are equal. Two triangles are said to be congruent if and only if they can be overlapped with each other completely. In this article, we are going to learn about the different criteria for the Congruence of Triangles with the help of solved examples. Congruent triangles are triangles that are perfect copies of one another. Various congruence rules are used to prove the congruency in two triangles. Congruent triangles if arranged in proper orientation are mirror images of each other.

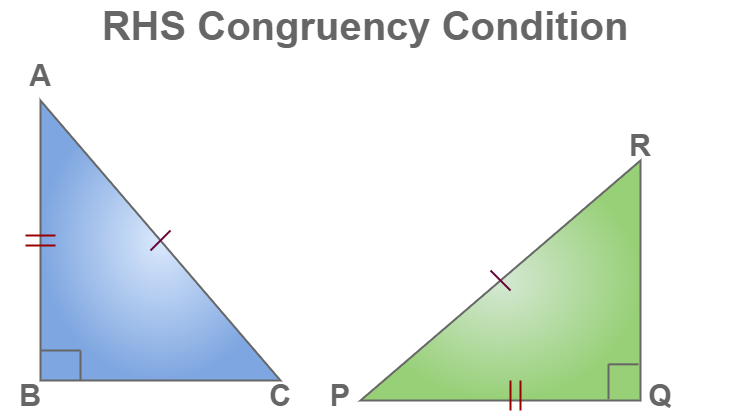
As an avid student of geometry, you likely understand the importance of congruence in shapes and figures. One of the most fundamental rules for determining congruence is the rhs congruence rule. Mastering this rule will open a deeper understanding of triangle congruence and similarity, providing a foundation for more complex geometric proofs and problem solving. In this article, you will explore the rhs congruence rule in detail. Beginning with the definition and formula, you will then see step-by-step how to apply the rule through examples and practice problems. With consistent application of the rhs congruence rule, you will strengthen your geometric reasoning and build confidence in your ability to determine congruence between triangles. Read on to discover how this essential rule of geometry will expand your mathematical skills. The RHS Congruence Rule states that if two right triangles have hypotenuses and a pair of corresponding sides that are equal, then the triangles are congruent. To understand this rule,. It allows you to prove whether two right triangles are congruent if their hypotenuses and one pair of corresponding sides are equal.

Rhs congruence rule examples

Congruence of triangles: Two triangles are said to be congruent if all three corresponding sides are equal and all the three corresponding angles are equal in measure. These triangles can be slides, rotated, flipped and turned to be looked identical. If repositioned, they coincide with each other. T he meaning of congruence in Maths is when two figures are similar to each other based on their shape and size. There are basically four congruence rules that proves if two triangles are congruent. But it is necessary to find all six dimensions.

Comfort suites columbus west

Note that this theorem is only applicable to the right-angled triangles. The RHS Congruence Rule can be applied when we have to check if two right triangles are congruent, where we know the lengths of the hypotenuse and one side of the triangle. If all the three sides of one triangle are equivalent to the corresponding three sides of the second triangle, then the two triangles are said to be congruent by SSS rule. Important Notes on RHS 4. Additional Information. Saudi Arabia. Two objects or shapes are said to be congruent if they superimpose on each other. Please go through our recently updated Improvement Guidelines before submitting any improvements. Congruent triangles overlap each other completely. Congruent Triangles. Here are a few activities for you to practice. The different criteria used to prove congruency between two triangles are:. No, all similar triangles are not congruent, but all congruent triangles are similar. Thus, two triangles can be superimposed side to side and angle to angle.

Two triangles are said to be congruent to each other if the measurements of their three sides and their three angles are exactly the same. They may be rotated or flipped. But when you carve them in a piece of paper, cut them out and place one on top of the other, they cover each other perfectly.

We can also say if two shapes are congruent, then the mirror image of one shape is the same as the other. Count number of triangles cut by the given horizontal and vertical line segments. Post My Comment. What is SSS congruency of triangles? If all the three corresponding sides of two corresponding triangles are equal then the triangles are said to be congruent by SSS congruency condition. Inaya June 23, at pm. Admission Experiences. Relations And Functions. However, in order to be sure that the two triangles are congruent, we do not necessarily need to have information about all sides and all angles. Right-Hand-Side theorem.