Rhs similarity criterion

Now, let us discuss a rigorous proof of the RHS criterion. Is this possible?

If one of the acute angles of a right triangle is congruent to an acute angle of another right triangle, then by Angle-Angle Similarity the triangles are similar. If the lengths of the corresponding legs of two right triangles are proportional, then by Side-Angle-Side Similarity the triangles are similar. If the lengths of the hypotenuse and a leg of a right triangle are proportional to the corresponding parts of another right triangle, then the triangles are similar. You can prove this by using the Pythagorean Theorem to show that the third pair of sides is also proportional. Taking Leg-Leg Similarity and Hypotenus-Leg Similarity together, we can say that if any two sides of a right triangle are proportional to the corresponding sides of another right triangle, then the triangles are similar. Call Now to Set Up Tutoring.

Rhs similarity criterion

Things are often referred similar when the physical structure or patterns they show are having similar properties, Sometimes two objects may vary in size but because of their physical similarities, they are called similar objects. For example, a bigger Square will always be similar to a smaller square. In Triangles, if the sizes vary but the shape they have are alike, then the Triangles can be called Similar Triangles. When two triangles are declared Similar, their corresponding angles are always congruent Identical in form , and their sides are Proportional. Two or more than two triangles are similar when their corresponding angles are congruent and their sides are proportional to each other the ratio of their sides are equal. Noticing things from our daily life or a good look in our textbooks tell us that there are so many objects similar to each other we have never noticed, For Instance, a baby bear looks alike its mother even though the mother is relatively bigger, the same concept is applied here in triangles. If a line is drawn parallel to one side of a triangle, intersecting other sides at distinct points, then the division of the other two sides is in the same ratio. If a line divides any two sides of the triangle in the same ratio, then the line is parallel to the third side of the triangle. But, K and N lie on the same line PR, Therefore, they coincide each other and are just the same point. Two triangles are called similar when their angles are equal and their corresponding sides are always in the same ratio, this is what we have learned so far, however one does not need to prove all the things mentioned above to show similarity of two triangles.

For example, the SSS similarity test specifies that the matching sides of the two triangles are in a constant ratio, and the SSS congruence test rhs similarity criterion that the matching sides have equal length, that is, that the constant ratio is 1 : 1. Important Notes on RHS 4. The mini-lesson targeted the fascinating concept of RHS.

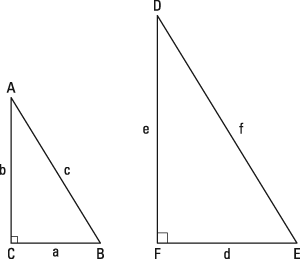
Two triangles are said to be congruent to each other if the measurements of their three sides and their three angles are exactly the same. They may be rotated or flipped. But when you carve them in a piece of paper, cut them out and place one on top of the other, they cover each other perfectly. Theorem: In two right-angled triangles, if the length of the hypotenuse and one side of one triangle, is equal to the length of the hypotenuse and corresponding side of the other triangle, then the two triangles are congruent. Theorem : In two triangles, if the three sides of one triangle are equal to the corresponding three sides SSS of the other triangle, then the two triangles are congruent. Show that BD bisects AC at right angles.

If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Search for courses, skills, and videos. Congruent triangles. About About this video Transcript. He also shows that AAA is only good for similarity. For SSA, better to watch next video. Created by Sal Khan. Want to join the conversation?

Rhs similarity criterion

Online Math Solver ». IntMath f orum ». In geometry, two figures are said to be "congruent" if they have the same size and shape. In other words, congruent figures can be superimposed on one another. Proving that two figures are congruent is often a key step in solving geometric problems. There are several different ways to prove that two figures are congruent. In this blog post, we'll focus on one particular method known as the "RHS congruence criterion", which is written in full as Right-Hand Side congruence criterion. The RHS criterion is used to determine if two right triangles are congruent. By this criterion, if the hypotenuse and one side of two right-angle triangles are the same, then the figures are congruent. Let's take a look at how this works with a few examples.

Skyrim skill book locations

Convert each scale to a ratio of lengths in the units indicated. If you fix two sides of a triangle and an angle not between them, there are two nonsimilar triangles with those measurements unless the two sides are congruent or the angle is right. Kim Seidel. The following exercise is intended to present two further examples of enlargements, and to confirm that in these two cases, each distance is increased by the enlargement factor. Exercise 5 In the two right-angled triangles in the diagram, the two hypotenuses are in the ratio 1 : k , and the sides AB and PQ are in the ratio 1 : k. Squidward Tentacles. Arch Colleges in Hyderabad M. E Colleges in Pune Top B. Criteria for Similarity of Triangles. E Colleges in Chennai B. Such a construction was the subject of Exercise 10, and we now redefine enlargement to be the result of this construction. Suggest changes. Branches BCA.

Now, let us discuss a rigorous proof of the RHS criterion. Is this possible?

For example, here is an alternative proof of the intersecting chord theorem above. Assumed Knowledge Motivation Content Scale drawings Enlargements Similarity Four similarity tests for triangles Similarity and intercept theorems Further applications of similarity Links Forward Similarity in circle geometry Similarity in trigonometry Similarity of other conic sections Enlargements and other transformations in coordinate geometry History and Applications Scale drawings Appendix A. We can develop each similarity test from the corresponding congruence test. Given that 1 Angstromunit is 10 metres, express this scale as the ratio of two numbers. So this will be the first of our similarity postulates. AAA referring to angles all three of the triangles. What SAS in the similarity world tells you is that these triangles are definitely going to be similar triangles, that we're actually constraining because there's actually only one triangle we can draw a right over here. This article is being improved by another user right now. Branches BCA. Distributive Property. Here are a few activities for you to practice. Thus a scale drawing of a two-dimensional object, and an enlargement of a plane figure, bith produce figures similar to the original. Similar College. Call Now to Set Up Tutoring.