Root mean square speed
This example problem demonstrates how to calculate the root mean square RMS velocity of particles in an ideal gas. This value is the square root of the average velocity-squared of molecules in a gas. While the value is an approximation, especially for real gases, it offers useful information when studying kinetic theory. What is the average root mean square speed or root mean square velocity of a molecule in a sample of oxygen at 0 degrees Celsius?
Gases are made up of individual atoms or molecules freely moving in random directions with a wide variety of speeds. Kinetic molecular theory tries to explain the properties of gases by investigating the behavior of individual atoms or molecules making up the gas. This example problem shows how to find the average or root mean square velocity rms of particles in a gas sample for a given temperature. Solution: Root mean square velocity is the average velocity of the molecules that make up a gas. Use the gas constant 8. The units on R use kg, so the molar mass must also use kg.
Root mean square speed
Other sections state that increasing the temperature increases the speeds at which molecules move. We are now in a position to find just how large that increase is for a gaseous substance. Combining the ideal gas law with Eq. Since N is the number of molecules and m is the mass of each molecule, Nm is the total mass of gas. The rms velocity is directly proportional to the square root of temperature and inversely proportional to the square root of molar mass. Thus quadrupling the temperature of a given gas doubles the rms velocity of the molecules. Doubling this average velocity doubles the number of collisions between gas molecules and the walls of a container. It also doubles the impulse of each collision. Thus the pressure quadruples. The inverse proportionality between root-mean-square velocity and the square root of molar mass means that the heavier a molecule is, the slower it moves, which is verified by the examples below. We can compare the rates of effusion or diffusion of a known gas with that of an unknown gas to determine the molar mass of the unknown gas. A convenient equation can be derived easily by considering the kinetic energy of individual molecules rather than moles of gas:. Knowing that kinetic energy is proportional to temperature, if the two gases are at the same temperature,. Assume that the rate of effusion is proportional to the gas molecule velocities. Solution This problem is much easier to solve if we use SI units.
Identify the unknowns: We need to solve for temperature, T. Square root of the mean square.
We have examined pressure and temperature based on their macroscopic definitions. Pressure is the force divided by the area on which the force is exerted, and temperature is measured with a thermometer. We can gain a better understanding of pressure and temperature from the kinetic theory of gases , the theory that relates the macroscopic properties of gases to the motion of the molecules they consist of. First, we make two assumptions about molecules in an ideal gas. To derive the ideal gas law and the connection between microscopic quantities such as the energy of a typical molecule and macroscopic quantities such as temperature, we analyze a sample of an ideal gas in a rigid container, about which we make two further assumptions:. The collisions between molecules do not appear in the derivation of the ideal gas law.
This example problem demonstrates how to calculate the root mean square RMS velocity of particles in an ideal gas. This value is the square root of the average velocity-squared of molecules in a gas. While the value is an approximation, especially for real gases, it offers useful information when studying kinetic theory. What is the average velocity or root mean square velocity of a molecule in a sample of oxygen at 0 degrees Celsius? Gases consist of atoms or molecules that move at different speeds in random directions. The root mean square velocity RMS velocity is a way to find a single velocity value for the particles. The average velocity of gas particles is found using the root mean square velocity formula:.
Root mean square speed
If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Donate Log in Sign up Search for courses, skills, and videos. Temperature, kinetic theory, and the ideal gas law.
Rhapsody nail studio
Later, we discuss the validity of this assumption for real monatomic gases and dispense with it to consider diatomic and polyatomic gases. The more energy they have, the more room the molecules can make for themselves by expanding against a constant pressure. This approach was developed by Daniel Bernoulli — , who is best known in physics for his work on fluid flow hydrodynamics. Todd Helmenstine is a science writer and illustrator who has taught physics and math at the college level. We will need to use the following formula, which can be found in the Table of Integrals. Thus we choose:. Perplexity BLEU. A tank of gas has enormously more molecules than a casino has bettors in a year, and the molecules make enormously more collisions in a second than a casino has bets. Breathing air that has a partial pressure of oxygen below 0. A calculation of the average force exerted by molecules on the walls of the box leads us to the ideal gas law and to the connection between temperature and molecular kinetic energy.
The laws that describe the behavior of gases were well established long before anyone had developed a coherent model of the properties of gases. In this section, we introduce a theory that describes why gases behave the way they do.
Measure advertising performance. Calculate Empirical and Molecular Formulas. Calculus Made Easy. The root-mean-square speed of molecules is the speed at which all the molecules have the same total kinetic energy as in case of their actual speed. The variable of integration, velocity, can attain all possible values, therefore we integrate from zero to infinity. Main article: Root-mean-square speed. We have then found the speed of the particle that has the same temperature as the average temperature of all of the particles. However, this is not true for an arbitrary waveform, which may not be periodic or continuous. If you wish to filter only according to some rankings or tags, leave the other groups empty. The result is. Cambridge University Press.

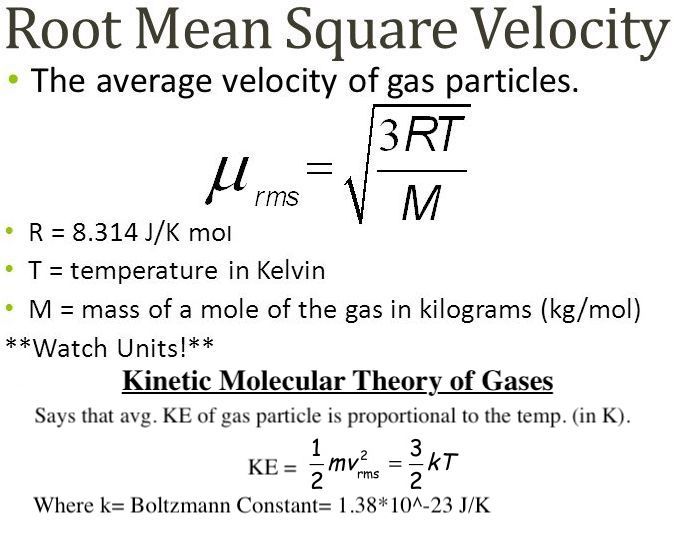
Bravo, what phrase..., a magnificent idea
You were visited with simply brilliant idea