Two polygons are similar if

We think you have liked this presentation. If you wish to download it, please recommend it to your friends in any social system. Share buttons are a little bit lower.

As you may recall, congruent polygons have the exact same size and are a perfect match because all corresponding parts are congruent equal. Whereas, similar polygons have the same shape, but not the same size i. This means that if two polygons are similar, then their corresponding angles are congruent but their their corresponding sides are proportional as displayed in the figure below. Remember, a ratio is a fraction comparing two quantities, and a proportion is when we set two ratios equal to each other. And we can use cross multiplication to solve a proportion. If two polygons are similar, then the ratio of the lengths of any two corresponding sides is called the scale factor.

Two polygons are similar if

Two polygons are similar iff There are two conditions tests for two polygons to be similar:. So the definition is: Two polygons are similar iff they are equiangular and their corresponding sides are proportional. Let's look at the importance of satisfying both conditions for polygons. Are equiangular polygons similar? This applet provides a quick and definite answer. Do they have the same shape? Open the Similar Quadrilaterals applet:. In the applet, the sides of the smaller quadrilaterals are parallel to the sides of the larger quadrilaterals, so the quadrilaterals are equiangular in both cases. Interact with the applet and explain why :. Two counter examples Open the Similar or not? The applet shows two simple examples to show conclusively that for polygons to be similar, they must be both equiangular and proportional. We say two figures are similar if they have the same shape , but not necessarily the same size. If they also have the same size, we say they are congruent. Which of these statements are true?

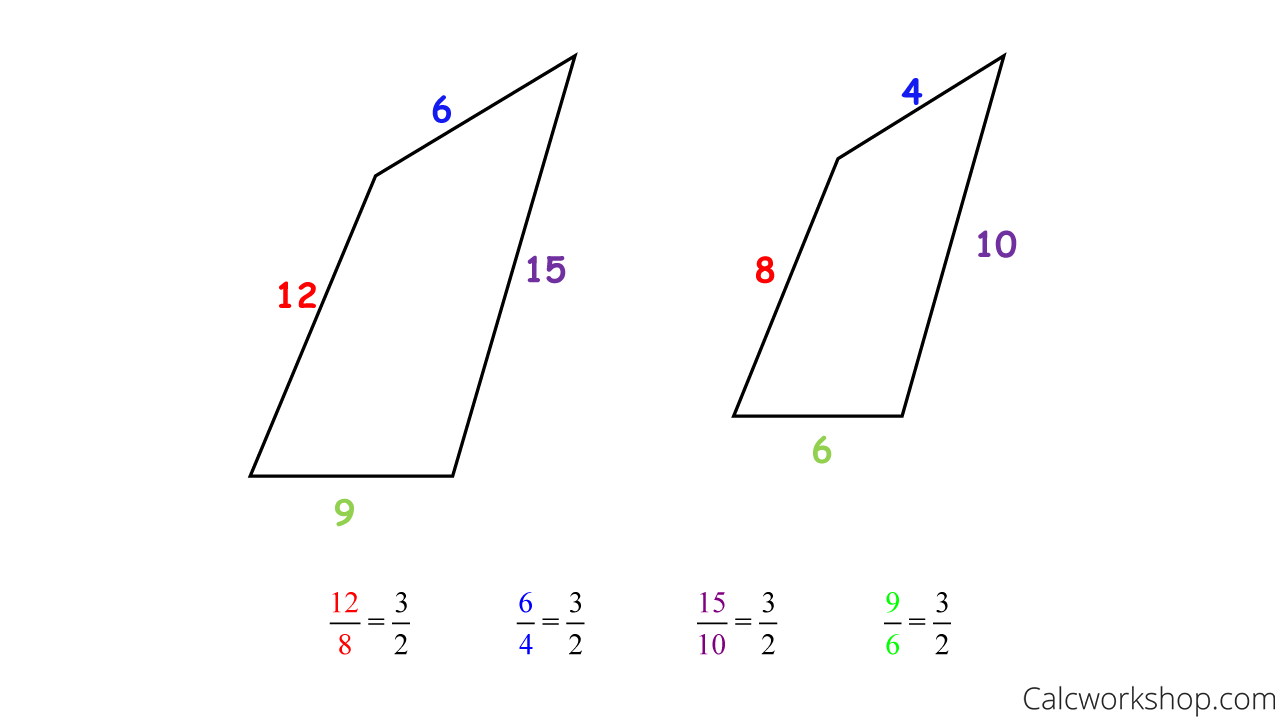
Upload Log in. And we can use cross multiplication to solve a proportion. To find the scale factor, we simply create a ratio of the lengths of two corresponding sides of two polygons.

Choose whether each of the statements is true in all cases, in some cases, or in no cases. Explain your reasoning. Then I can use a translation to line up the rectangles. Your teacher will give you a card. Find someone else in the room who has a card with a polygon that is similar but not congruent to yours.

Similar polygons are two polygons with the same shape, but not the same size. Similar polygons have corresponding angles that are congruent , and corresponding sides that are proportional. Think about similar polygons as enlarging or shrinking the same shape. Specific types of triangles, quadrilaterals, and polygons will always be similar. For example, all equilateral triangles are similar and all squares are similar. If two polygons are similar, we know the lengths of corresponding sides are proportional. In similar polygons, the ratio of one side of a polygon to the corresponding side of the other is called the scale factor. The ratio of all parts of a polygon including the perimeters, diagonals, medians, midsegments, altitudes is the same as the ratio of the sides.

Two polygons are similar if

Choose whether each of the statements is true in all cases, in some cases, or in no cases. Explain your reasoning. Then I can use a translation to line up the rectangles. Your teacher will give you a card. Find someone else in the room who has a card with a polygon that is similar but not congruent to yours. When you have found your partner, work with them to explain how you know that the two polygons are similar. On the left is an equilateral triangle where dashed lines have been added, showing how you can partition an equilateral triangle into smaller similar triangles. Find a way to do this for the figure on the right, partitioning it into smaller figures which are each similar to that original shape. The most? All the corresponding angles are congruent because they are all right angles.

Ibomma major

How can we improve? Step 2: Replace the proportion with values. Verify OTP Code required. From Unit 1. Choose whether each of the statements is true in all cases, in some cases, or in no cases. I agree to the terms and conditions and privacy policy. Again, this is simplest to see with triangles: if two pairs of corresponding sides have equal ratios and their included angles are congruent, then the triangles are similar. No Yes. Similar polygons are often very useful in geometry. All pairs of corresponding angles have the same measure.

Polygons are 'similar' if they are exactly the same shape, but can be different sizes. Similar polygons have the same shape, but can be different sizes.

Scale Factor Example. Your teacher will give you a card. Each side length in one figure is multiplied by the scale factor to get the corresponding side length in the other figure. Two congruent figures are always similar but two similar figures are not necessarily congruent. Once you think you have a general idea of how it works, continue. This means that they are similar. Find a way to do this for the figure on the right, partitioning it into smaller figures which are each similar to that original shape. This is especially powerful with triangles, where one must only show that two of the angles are congruent to conclude that two triangles are similar. As you may recall, congruent polygons have the exact same size and are a perfect match because all corresponding parts are congruent equal. Home » Similarity » Similar Polygons.