What is the reciprocal ratio of sine

The reciprocal of sine is the cosecant function. There are six main trigonometric functions namely, sine, cosine, tangent, cotangent, secant, and cosecant. An important thing to note is that the reciprocal of sine is not the inverse function of sine, that is, the cosecant function is not the inverse function of sine.

Trigonometry is all about triangles or to be more precise about the relation between the angles and sides of a right-angled triangle. In this article, we will be discussing about the ratio of sides of a right-angled triangle with respect to its acute angle called trigonometric ratios of the angle and find the reciprocals of these Trigonometric Ratios. The trigonometric ratios of an acute angle in a right triangle are the relationship between the angle and the length of two sides. The ratios defined below are abbreviated as sin C, cos C, and tan C respectively. Reciprocals of basic trigonometric ratios are the inverse values of the sin, cos, and tan values that are computed by reciprocating the sides required for computing the ratio.

What is the reciprocal ratio of sine

If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Search for courses, skills, and videos. The reciprocal trigonometric ratios. About About this video Transcript. Sal finds all six trigonometric ratios sine, cosine, tangent, secant, cosecant, and cotangent of an angle in a given right triangle. Created by Sal Khan. Want to join the conversation? Log in. Sort by: Top Voted. Posted 11 years ago.

What are the applications of trigonometry in real life? Open In App.

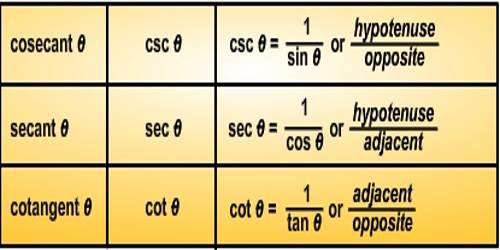
The six trigonometric ratios are sine, cosine, tangent, cotangent, secant, cosecant, out of which the three standard trigonometric ratios are sine, cosine, and tangent. The six trigonometric ratios can be grouped in pairs as reciprocals. The reciprocal identities are the reciprocals of these six trigonometric ratios. Note that reciprocal identities are not the same as inverse trigonometric functions. Reciprocal identities are the reciprocals of the six fundamental trigonometric functions sine, cosine, tangent, secant, cosecant, and cotangent. It is obtained by interchanging the values of numerator and denominator.

Online Trigonometry Solver ». IntMath f orum ». Often it is useful to use the reciprocal ratios, depending on the problem. In plain English, the reciprocal of a fraction is found by turning the fraction upside down. In some textbooks, " csc " is written as " cosec ". It's the same thing. An angle in standard position. For an angle in standard position , we define the trigonometric ratios in terms of x , y and r :. We can choose any point on that line, of course, to define our ratios. Not surprisingly, the reciprocal ratios are defined similarly in terms of the x -, y - and r -values as follows:.

What is the reciprocal ratio of sine

Suppose you want to build a ramp for access to a loading dock that is 4 feet above ground level. How long does the ramp have to be? In this diagram, you have a right triangle for which you know the length of one side and the measure of an acute angle. You want to find the length of the hypotenuse.

Fire emblem engage unit tier list

It's length 5. The reciprocal of sine is the ratio of the hypotenuse and the opposite side of a right-angled triangle. And then we can get the other three by looking at the first three. Suggest Changes. Posted 4 years ago. What Are Trigonometric Reciprocal Identities? Already booked a tutor? Related Articles. Hence, cosecant is the reciprocal of sine. David Calkins. Get paid for your published articles and stand a chance to win tablet, smartwatch and exclusive GfG goodies! Thank you for your valuable feedback! So this right over here is the hypotenuse. View More.

If you're seeing this message, it means we're having trouble loading external resources on our website. To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Learn Practice Download. Consider the following triangle:. In this article, we explored different reciprocal identities, their formulas, and proof. Now, that we have studied many facts and formulas of the reciprocal of sine, let us go through some of the important properties of the reciprocal of sine:. Save Article Save. Explore math program. So instead of being adjacent over hypotenuse, which we got from the cah part of soh cah toa, it's hypotenuse over adjacent. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. Our Journey. David Calkins. Show preview Show formatting options Post answer. Privacy Policy. But where do we use them!! Domain and Range of Reciprocal of Sine 4.