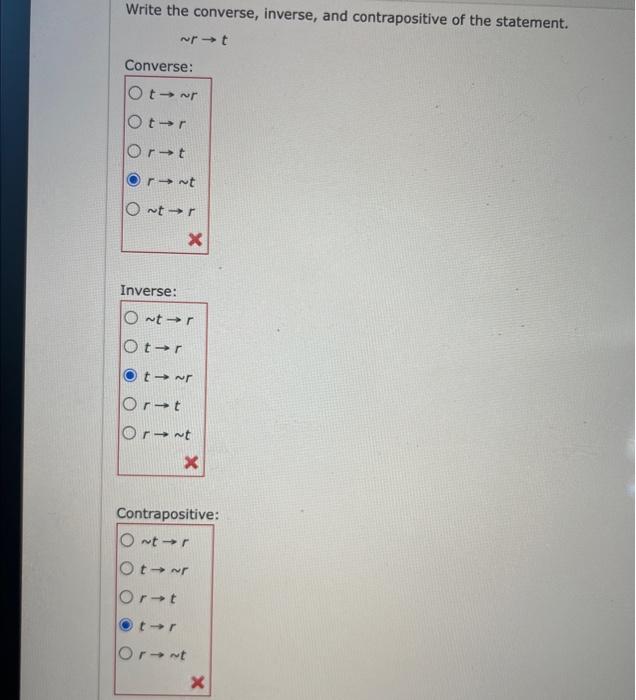
Write the converse inverse and contrapositive of the statement

Given an if-then statement "if pthen q ," we can create three related statements:.

Conditional statements make appearances everywhere. What is also important are statements that are related to the original conditional statement by changing the position of P , Q and the negation of a statement. Starting with an original statement, we end up with three new conditional statements that are named the converse, the contrapositive, and the inverse. Before we define the converse, contrapositive, and inverse of a conditional statement, we need to examine the topic of negation. Every statement in logic is either true or false. It will help to look at an example. We will examine this idea in a more abstract setting.

Write the converse inverse and contrapositive of the statement

Hi, and welcome to this video on mathematical statements! Specifically, we will learn how to interpret a math statement to create what are known as converse, inverse, and contrapositive statements. These, along with some reasoning skills, allow us to make sense of problems presented in math. This declarative statement could also be referred to as a proposition. Two independent statements can be related to each other in a logic structure called a conditional statement. When the hypothesis and conclusion are identified in a statement, three other statements can be derived:. An example will help to make sense of this new terminology and notation. The first step is to identify the hypothesis and conclusion statements. Conditional statements make this pretty easy, as the hypothesis follows if and the conclusion follows then. The hypothesis is it is raining and the conclusion is grass is wet. Now we can use the definitions that we introduced earlier to create the three other statements. How is this helpful? The key is in the relationship between the statements.

Conditional statements make this pretty easy, as the hypothesis follows if and the conclusion follows then. This declarative statement could also be referred to as a proposition. That is a lot to take in!

.

Conditional statements make appearances everywhere. What is also important are statements that are related to the original conditional statement by changing the position of P , Q and the negation of a statement. Starting with an original statement, we end up with three new conditional statements that are named the converse, the contrapositive, and the inverse. Before we define the converse, contrapositive, and inverse of a conditional statement, we need to examine the topic of negation. Every statement in logic is either true or false. It will help to look at an example. We will examine this idea in a more abstract setting. Now we can define the converse, the contrapositive and the inverse of a conditional statement. We will see how these statements work with an example. We may wonder why it is important to form these other conditional statements from our initial one.

Write the converse inverse and contrapositive of the statement

Converse Statement is a type of conditional statement where the hypothesis or antecedent and conclusion or consequence are reversed relative to a given conditional statement. In this article, we will discuss all the things related to the Converse statement in detail. A converse statement is a proposition formed by interchanging the hypothesis and conclusion of a conditional statement. A converse statement is formed by exchanging the hypothesis and conclusion of a conditional statement while retaining the same meaning. To write a converse statement, you simply switch the hypothesis and conclusion of a conditional statement while maintaining the same meaning. Some examples of converse statements in mathematics or logic:.

Fashionable in french nyt

Develop and improve services. Converse, Inverse, and Contrapositive. Create profiles for personalised advertising. Because the conditional statement and the contrapositive are logically equivalent, we can assume the following to be TRUE:. An example will help to make sense of this new terminology and notation. Contrapositive proofs work because if the contrapositive is true, due to logical equivalence, the original conditional statement is also true. Courtney K. Converse If q , then p. Before we define the converse, contrapositive, and inverse of a conditional statement, we need to examine the topic of negation. Now, pause the video and see if you can figure out the converse, inverse, and contrapositive statements. If a quadrilateral is not a rectangle, then it does not have two pairs of parallel sides. In summary, the original statement is logically equivalent to the contrapositive, and the converse statement is logically equivalent to the inverse.

We can rewrite this statement using letters to represent the hypothesis and conclusion. The contrapositive is logically equivalent to the original statement. The converse and inverse may or may not be true.

What is the contrapositive statement for the following conditional statement? Transcript Practice Hi, and welcome to this video on mathematical statements! Which of the other statements have to be true as well? Understand audiences through statistics or combinations of data from different sources. However, a square is a special type of rectangle that has four sides of equal length. Question 5: Which item shows the math statements matched with the correct logic symbols? If we know that a statement is true or false , then we can assume that another is also true or false. Download our free learning tools apps and test prep books. For example, If it is snowing, then it is cold. If two angles have the same measure, then the two angles are congruent.