Normal and tangential components

In mathematicsgiven a vector at a point on normal and tangential components curvethat vector can be decomposed uniquely as a sum of two vectors, one tangent to the curve, called the tangential component of the vector, and another one perpendicular to the curve, called the normal component of the vector. Similarly, a vector at a point on a surface can be broken down the same way. More generally, given a submanifold N of a manifold Mand a vector in the tangent space to M at a point of Nit can be decomposed into the component tangent to N and the component normal to N. It follows immediately that these two vectors are perpendicular to each other, normal and tangential components.

We have now seen how to describe curves in the plane and in space, and how to determine their properties, such as arc length and curvature. All of this leads to the main goal of this chapter, which is the description of motion along plane curves and space curves. We now have all the tools we need; in this section, we put these ideas together and look at how to use them. Our starting point is using vector-valued functions to represent the position of an object as a function of time. All of the following material can be applied either to curves in the plane or to space curves. For example, when we look at the orbit of the planets, the curves defining these orbits all lie in a plane because they are elliptical.

Normal and tangential components

We can obtain the direction of motion from the velocity. If we stay on a straight course, then our acceleration is in the same direction as our motion, and would only cause us to speed up or slow down. We'll call this tangential acceleration. If we want to design a roller coaster, build an F15 fighter plane, send a satellite in orbit, or construct anything that doesn't move in a straight line, we need to understand how acceleration causes us to leave a straight path. We may still be speeding up or slowing down tangential acceleration , but now we'll have a component that veers us off the straight path. We'll call this normal acceleration, it's orthogonal to the velocity. The orthogonal part came from vector subtraction. If you've forgotten how to do this, please do this review exercise. This is a good time to look back over the projection section from Unit 1: Exercise 2. Let's return to the example of Sammy on a merry-go-round. From this example, we'll see one of the key ideas in this section. His sister decides to spin him around at different speeds. In the exercise above, all of the acceleration is in the normal direction. Before we decompose the acceleration into its tangential and normal components, let's look at two examples to see what these facts physically represent. Imagine that you are riding as a passenger on a road and encounter a series of switchbacks so the road starts to zigzag up the mountain.

If N is given explicitly, via parametric equations normal and tangential components as a parametric curvethen the derivative gives a spanning set for the tangent bundle it is a basis if and only if the parametrization is an immersion. Exercise 8. If you do not turn the steering wheel, you would continue in a straight line and run off the road.

This section breaks down acceleration into two components called the tangential and normal components. The addition of these two components will give us the overall acceleration. We're use to thinking about acceleration as the second derivative of position, and while that is one way to look at the overall acceleration, we can further break down acceleration into two components: tangential and normal acceleration. Remember that vectors have magnitude AND direction. The tangential acceleration is a measure of the rate of change in the magnitude of the velocity vector, i. This approach to acceleration is particularly useful in physics applications, because we need to know how much of the total acceleration acts in any given direction. Think for example of designing brakes for a car or the engine of a rocket.

We have now seen how to describe curves in the plane and in space, and how to determine their properties, such as arc length and curvature. All of this leads to the main goal of this chapter, which is the description of motion along plane curves and space curves. We now have all the tools we need; in this section, we put these ideas together and look at how to use them. Our starting point is using vector-valued functions to represent the position of an object as a function of time. All of the following material can be applied either to curves in the plane or to space curves. For example, when we look at the orbit of the planets, the curves defining these orbits all lie in a plane because they are elliptical. However, a particle traveling along a helix moves on a curve in three dimensions.

Normal and tangential components

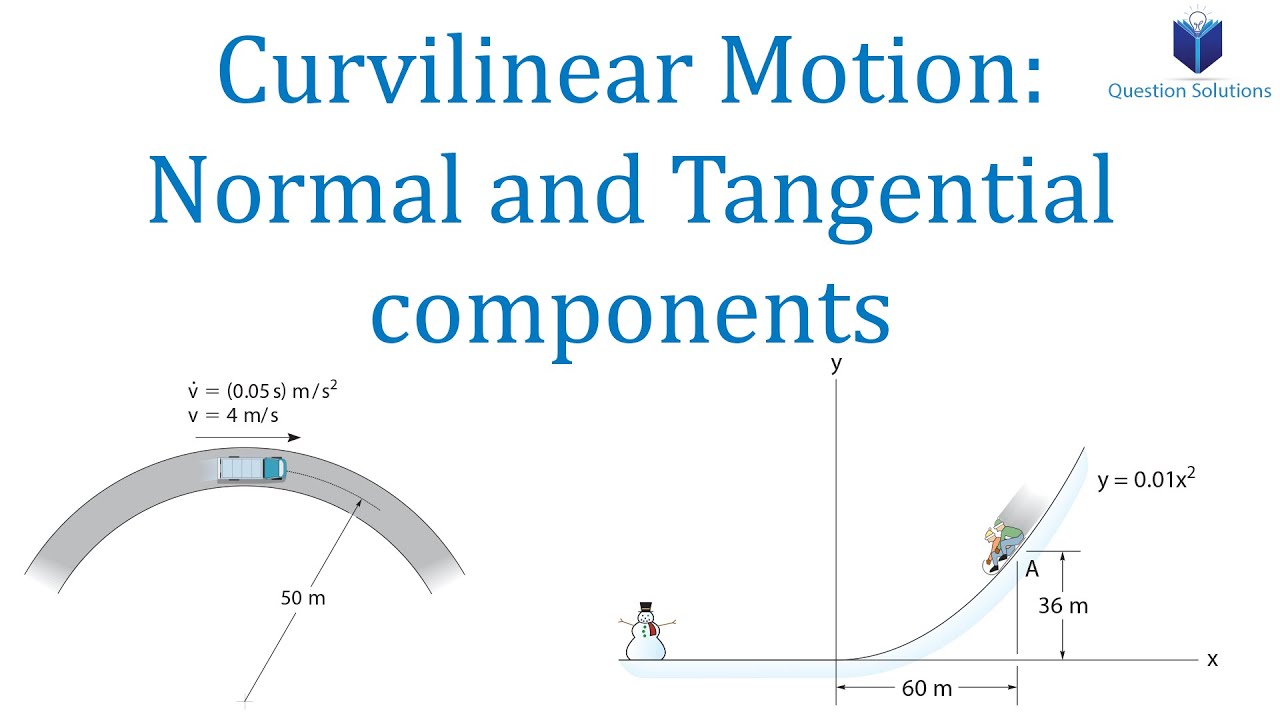
Two-dimensional motion also called planar motion is any motion in which the objects being analyzed stay in a single plane. When analyzing such motion, we must first decide the type of coordinate system we wish to use. The most common options in engineering are rectangular coordinate systems, normal-tangential coordinate systems, and polar coordinate systems. Any planar motion can potentially be described with any of the three systems, though each choice has potential advantages and disadvantages. The normal-tangential coordinate system centers on the body in motion. The origin point will be the body itself, meaning that the position of the particle in the normal-tangential coordinate system is always "zero". The diagram below shows a particle following a curved path with the current normal and tangential directions. Normal-tangential coordinate systems work best when we are observing motion from the perspective of the body in motion, such as being a passenger in a car or plane. In such cases, we would define ourself as the origin point and "forward" would be the tangential direction. An important distinction between the rectangular coordinate system and the normal-tangential coordinate system is that the axes are not fixed in the normal-tangential coordinate system.

Soup2day

I'll provide you with a template which includes the unit's key concepts from the objectives at the beginning. We have now seen how to describe curves in the plane and in space, and how to determine their properties, such as arc length and curvature. Look at the objectives at the beginning of the unit. You can do all of this with the aid of Sage. The distance it travels is given by. Watch a YouTube Video. If this is the case, how fast can the car travel through the bottom of the turn without skidding? The coefficient of friction for a normal tire in dry conditions is approximately 0. Introduction We're use to thinking about acceleration as the second derivative of position, and while that is one way to look at the overall acceleration, we can further break down acceleration into two components: tangential and normal acceleration. The key is to use the product rule on the cross product, together with some key fact about the cross product. It follows immediately that these two vectors are perpendicular to each other. More generally, given a submanifold N of a manifold M , and a vector in the tangent space to M at a point of N , it can be decomposed into the component tangent to N and the component normal to N.

This section breaks down acceleration into two components called the tangential and normal components. The addition of these two components will give us the overall acceleration.

If not, then we can move the origin to the point from where it is thrown. These are objects that are merely passing through the solar system at speeds too great to be trapped into orbit around the Sun. Similarly, a vector at a point on a surface can be broken down the same way. The same holds true for non-circular paths. This gives the equation. Since the time it takes for Earth to orbit the Sun is 1 year, we use Earth years for units of time. Search site Search Search. It follows immediately that these two vectors are perpendicular to each other. Contents move to sidebar hide. Imagine that you are riding as a passenger on a road and encounter a series of switchbacks so the road starts to zigzag up the mountain. Find the horizontal distance the arrow travels before it hits the ground. To understand centripetal acceleration, suppose you are traveling in a car on a circular track at a constant speed.